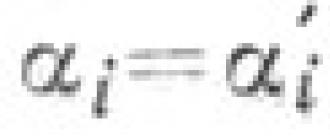Ինչպես գտնել բարդ ֆունկցիայի ածանցյալը: Բարդ ֆունկցիաների տարբերակում. Մաթեմատիկայի միասնական պետական քննությանը նախապատրաստվելու պրակտիկ առաջադրանք. Հզոր-էքսպոնենցիալ ֆունկցիայի ածանցյալ
Տրված է ածանցյալ բանաձևի ապացույց բարդ գործառույթ. Մանրամասն դիտարկվում են այն դեպքերը, երբ բարդ ֆունկցիան կախված է մեկ կամ երկու փոփոխականից։ Կատարվում է ընդհանրացում կամայական թվով փոփոխականների դեպքում:
ԲովանդակությունՏես նաեւ: Բարդ ֆունկցիայի ածանցյալի բանաձևի օգտագործման օրինակներ
Հիմնական բանաձևեր
Ներկայացնում ենք եզրակացությունը հետևյալ բանաձևերըբարդ ֆունկցիայի ածանցյալի համար։
Եթե, ապա
.
Եթե, ապա
.
Եթե, ապա
.
Բարդ ֆունկցիայի ածանցյալ մեկ փոփոխականից
Թող x փոփոխականի ֆունկցիան ներկայացվի որպես բարդ ֆունկցիա հետևյալ ձևով.
,
որտեղ կան որոշ գործառույթներ. Ֆունկցիան տարբերելի է x փոփոխականի որոշ արժեքների համար։ Ֆունկցիան տարբերելի է փոփոխականի արժեքով:
Այնուհետև բարդ (կոմպոզիտային) ֆունկցիան տարբերակելի է x կետում և դրա ածանցյալը որոշվում է բանաձևով.
(1)
.
Բանաձև (1) կարելի է գրել նաև հետևյալ կերպ.
;
.
Ապացույց
Ներկայացնենք հետևյալ նշումը.
;
.
Այստեղ կա փոփոխականների ֆունկցիա և , կա փոփոխականների ֆունկցիա և . Բայց մենք բաց կթողնենք այս ֆունկցիաների փաստարկները, որպեսզի չխառնվենք հաշվարկները։
Քանի որ ֆունկցիաները և տարբերվում են x և , համապատասխանաբար կետերում, ապա այս կետերում կան այդ ֆունկցիաների ածանցյալները, որոնք հետևյալ սահմաններն են.
;
.
Դիտարկենք հետևյալ գործառույթը.
.
U փոփոխականի ֆիքսված արժեքի ֆունկցիան է: Ակնհայտ է, որ
.
Հետո
.
Քանի որ ֆունկցիան տվյալ կետում տարբերվող ֆունկցիա է, այդ կետում այն շարունակական է: Ահա թե ինչու
.
Հետո
.
Այժմ մենք գտնում ենք ածանցյալը:
.
Բանաձևն ապացուցված է.
Հետևանք
Եթե x փոփոխականի ֆունկցիան կարող է ներկայացվել որպես բարդ ֆունկցիայի կոմպլեքս ֆունկցիա
,
ապա դրա ածանցյալը որոշվում է բանաձևով
.
Այստեղ և կան մի քանի տարբերակվող ֆունկցիաներ:
Այս բանաձևն ապացուցելու համար մենք հաջորդաբար հաշվարկում ենք ածանցյալը՝ օգտագործելով բարդ ֆունկցիայի տարբերակման կանոնը:
Դիտարկենք բարդ ֆունկցիան
.
Դրա ածանցյալը
.
Դիտարկենք բնօրինակ գործառույթը
.
Դրա ածանցյալը
.
Կոմպլեքս ֆունկցիայի ածանցյալը երկու փոփոխականից
Հիմա թող կոմպլեքս ֆունկցիան կախված լինի մի քանի փոփոխականներից: Նախ եկեք նայենք երկու փոփոխականների բարդ ֆունկցիայի դեպք.
Թող x փոփոխականից կախված ֆունկցիան ներկայացվի որպես երկու փոփոխականների բարդ ֆունկցիա հետևյալ ձևով.
,
Որտեղ
և կան տարբերակելի ֆունկցիաներ x փոփոխականի որոշ արժեքների համար;
- երկու փոփոխականների ֆունկցիա, որը տարբերվում է կետում, . Այնուհետև բարդ ֆունկցիան սահմանվում է կետի որոշակի հարևանությամբ և ունի ածանցյալ, որը որոշվում է բանաձևով.
(2)
.
Ապացույց
Քանի որ ֆունկցիաները և տարբերվում են կետում, դրանք սահմանված են այս կետի որոշակի հարևանությամբ, կետում շարունակական են, և դրանց ածանցյալները գոյություն ունեն այդ կետում, որոնք հետևյալ սահմաններն են.
;
.
Այստեղ
;
.
Այս գործառույթների շարունակականության շնորհիվ մի կետում մենք ունենք.
;
.
Քանի որ ֆունկցիան տվյալ կետում տարբերակելի է, այն սահմանվում է այս կետի որոշակի հարևանությամբ, այս կետում շարունակական է, և դրա աճը կարող է գրվել հետևյալ ձևով.
(3)
.
Այստեղ
- ֆունկցիայի ավելացում, երբ նրա արգումենտներն ավելանում են արժեքներով և .
;
- ֆունկցիայի մասնակի ածանցյալները փոփոխականների նկատմամբ և .
and-ի ֆիքսված արժեքների համար և են փոփոխականների ֆունկցիաները և. Նրանք հակված են զրոյի և.
;
.
ի վեր և, այնուհետև
;
.
Ֆունկցիայի ավելացում.
.
:
.
Եկեք փոխարինենք (3):
.
Բանաձևն ապացուցված է.
Բարդ ֆունկցիայի ածանցյալ մի քանի փոփոխականներից
Վերոհիշյալ եզրակացությունը հեշտությամբ կարելի է ընդհանրացնել այն դեպքին, երբ բարդ ֆունկցիայի փոփոխականների թիվը երկուսից ավելի է։
Օրինակ, եթե f-ն է երեք փոփոխականների ֆունկցիա, Դա
,
Որտեղ
, և կան տարբերվող ֆունկցիաներ x փոփոխականի որոշ արժեքների համար;
- երեք փոփոխականների տարբերակելի ֆունկցիա՝ կետում, , .
Այնուհետև ֆունկցիայի տարբերակելիության սահմանումից ունենք.
(4)
.
Որովհետև շարունակականության պատճառով.
;
;
,
Դա
;
;
.
Բաժանելով (4) և անցնելով սահմանին, մենք ստանում ենք.
.
Եվ վերջապես, եկեք դիտարկենք ամենաընդհանուր դեպքը.
Թող x փոփոխականի ֆունկցիան ներկայացվի որպես n փոփոխականի բարդ ֆունկցիա հետևյալ ձևով.
,
Որտեղ
կան տարբերակելի ֆունկցիաներ x փոփոխականի որոշ արժեքների համար.
- n փոփոխականների տարբերակելի ֆունկցիա մի կետում
,
,
... , .
Հետո
.
Եթե հետևում եք սահմանմանը, ապա մի կետում ֆունկցիայի ածանցյալը Δ ֆունկցիայի աճի հարաբերակցության սահմանն է։ yարգումենտի ավելացման Δ x:
Ամեն ինչ կարծես պարզ է. Բայց փորձեք այս բանաձևով հաշվարկել, ասենք, ֆունկցիայի ածանցյալը զ(x) = x 2 + (2x+ 3) · ե xմեղք x. Եթե դուք ամեն ինչ անում եք ըստ սահմանման, ապա մի երկու էջ հաշվարկներից հետո դուք պարզապես կքնեք։ Հետեւաբար, կան ավելի պարզ եւ արդյունավետ ուղիներ:
Սկզբից մենք նշում ենք, որ գործառույթների ամբողջ բազմազանությունից մենք կարող ենք առանձնացնել այսպես կոչված տարրական գործառույթները: Սրանք համեմատաբար պարզ արտահայտություններ են, որոնց ածանցյալները վաղուց հաշվարկված ու աղյուսակավորված են։ Նման գործառույթները բավականին հեշտ է հիշել՝ դրանց ածանցյալների հետ միասին:
Տարրական ֆունկցիաների ածանցյալներ
Տարրական գործառույթները բոլորն են, որոնք թվարկված են ստորև: Այս ֆունկցիաների ածանցյալները պետք է անգիր հայտնի լինեն։ Ավելին, դրանք անգիր անելն ամենևին էլ դժվար չէ, դրա համար էլ տարրական են։
Այսպիսով, ածանցյալներ տարրական գործառույթներ:
| Անուն | Գործառույթ | Ածանցյալ |
| Մշտական | զ(x) = Գ, Գ ∈ Ռ | 0 (այո, զրո!) |
| Հզորությունը ռացիոնալ ցուցիչով | զ(x) = x n | n · x n − 1 |
| Սինուս | զ(x) = մեղք x | cos x |
| Կոսինուս | զ(x) = cos x | − մեղք x(մինուս սինուս) |
| Շոշափող | զ(x) = տգ x | 1/co 2 x |
| Կոտանգենս | զ(x) = ctg x | − 1/մեղք 2 x |
| Բնական լոգարիթմ | զ(x) = գերան x | 1/x |
| Կամայական լոգարիթմ | զ(x) = գերան ա x | 1/(x ln ա) |
| Էքսպոնենցիալ ֆունկցիա | զ(x) = ե x | ե x(ոչինչ չի փոխվել) |
Եթե տարրական ֆունկցիան բազմապատկվում է կամայական հաստատունով, ապա նոր ֆունկցիայի ածանցյալը նույնպես հեշտությամբ հաշվարկվում է.
(Գ · զ)’ = Գ · զ ’.
Ընդհանրապես հաստատունները կարելի է հանել ածանցյալի նշանից։ Օրինակ:
(2x 3)' = 2 · ( x 3)' = 2 3 x 2 = 6x 2 .
Ակնհայտ է, որ տարրական գործառույթները կարելի է ավելացնել միմյանց, բազմապատկել, բաժանել և շատ ավելին: Այսպես կհայտնվեն նոր գործառույթներ՝ արդեն ոչ առանձնապես տարրական, այլ նաև տարբերակված՝ ըստ որոշակի կանոնների։ Այս կանոնները քննարկվում են ստորև:
Գումարի և տարբերության ածանցյալ
Թող տրվեն գործառույթները զ(x) Եվ է(x), որի ածանցյալները մեզ հայտնի են։ Օրինակ, կարող եք վերցնել վերը քննարկված տարրական գործառույթները: Այնուհետև կարող եք գտնել այս ֆունկցիաների գումարի և տարբերության ածանցյալը.
- (զ + է)’ = զ ’ + է ’
- (զ − է)’ = զ ’ − է ’
Այսպիսով, երկու ֆունկցիաների գումարի (տարբերության) ածանցյալը հավասար է ածանցյալների գումարին (տարբերությանը): Կարող են լինել ավելի շատ ժամկետներ: Օրինակ, ( զ + է + հ)’ = զ ’ + է ’ + հ ’.
Խիստ ասած, հանրահաշվում «հանում» հասկացություն չկա: Գոյություն ունի «բացասական տարր» հասկացություն։ Հետևաբար տարբերությունը զ − էկարող է վերագրվել որպես գումար զ+ (−1) է, և հետո մնում է միայն մեկ բանաձև՝ գումարի ածանցյալը։
զ(x) = x 2 + մեղք x; է(x) = x 4 + 2x 2 − 3.
Գործառույթ զ(x) երկու տարրական ֆունկցիաների գումարն է, հետևաբար.
զ ’(x) = (x 2 + մեղք x)’ = (x 2)’ + (մեղ x)’ = 2x+ cos x;
Մենք նմանապես հիմնավորում ենք ֆունկցիայի համար է(x). Միայն կան երեք տերմիններ (հանրահաշվի տեսանկյունից).
է ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).
Պատասխան.
զ ’(x) = 2x+ cos x;
է ’(x) = 4x · ( x
2 + 1).
Արտադրանքի ածանցյալ
Մաթեմատիկան տրամաբանական գիտություն է, ուստի շատերը կարծում են, որ եթե գումարի ածանցյալը հավասար է ածանցյալների գումարին, ապա արտադրանքի ածանցյալը. գործադուլ«>հավասար է ածանցյալների արտադրյալին: Բայց եղեք: Արտադրանքի ածանցյալը հաշվարկվում է բոլորովին այլ բանաձևով: Մասնավորապես.
(զ · է) ’ = զ ’ · է + զ · է ’
Բանաձևը պարզ է, բայց հաճախ մոռացվում է. Եվ ոչ միայն դպրոցականներ, այլեւ ուսանողներ։ Արդյունքը սխալ լուծված խնդիրներն են։
Առաջադրանք. Գտեք ֆունկցիաների ածանցյալները. զ(x) = x 3 cos x; է(x) = (x 2 + 7x− 7) · ե x .
Գործառույթ զ(x) երկու տարրական ֆունկցիաների արդյունք է, ուստի ամեն ինչ պարզ է.
զ ’(x) = (x 3 կո x)’ = (x 3)' cos x + x 3 (cos x)’ = 3x 2 կո x + x 3 (-մեղ x) = x 2 (3cos x − xմեղք x)
Գործառույթ է(x) առաջին գործոնը մի փոքր ավելի բարդ է, բայց ընդհանուր սխեմանսա չի փոխվում. Ակնհայտ է, որ ֆունկցիայի առաջին գործոնը է(x) բազմանդամ է և նրա ածանցյալը գումարի ածանցյալն է։ Մենք ունենք:
է ’(x) = ((x 2 + 7x− 7) · ե x)’ = (x 2 + 7x− 7)» · ե x + (x 2 + 7x- 7) ( ե x)’ = (2x+ 7) · ե x + (x 2 + 7x− 7) · ե x = ե x· (2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · ե x = x(x+ 9) · ե x .
Պատասխան.
զ ’(x) = x 2 (3cos x − xմեղք x);
է ’(x) = x(x+ 9) · ե
x
.
Խնդրում ենք նկատի ունենալ, որ վերջին քայլում ածանցյալը գործոնացվում է: Ֆորմալ կերպով դա պետք չէ անել, բայց ածանցյալների մեծ մասը հաշվարկվում է ոչ թե ինքնուրույն, այլ ֆունկցիան ուսումնասիրելու համար: Սա նշանակում է, որ հետագայում ածանցյալը կհավասարեցվի զրոյի, կորոշվեն նրա նշանները և այլն։ Նման դեպքի համար ավելի լավ է արտահայտությունը ֆակտորիզացված լինի։
Եթե կա երկու գործառույթ զ(x) Եվ է(x), և է(x) ≠ 0 մեզ հետաքրքրող բազմության վրա, կարող ենք նոր ֆունկցիա սահմանել հ(x) = զ(x)/է(x). Նման ֆունկցիայի համար կարող եք նաև գտնել ածանցյալը.
Թույլ չէ, չէ՞: Որտեղի՞ց եկավ մինուսը: Ինչո՞ւ է 2? Եվ այսպես. Սա ամենաբարդ բանաձևերից մեկն է. առանց շշի չես կարող հասկանալ: Ուստի ավելի լավ է այն ուսումնասիրել կոնկրետ օրինակներով։
Առաջադրանք. Գտեք ֆունկցիաների ածանցյալները.
Յուրաքանչյուր կոտորակի համարիչն ու հայտարարը պարունակում են տարրական ֆունկցիաներ, ուստի մեզ անհրաժեշտ է գործակիցի ածանցյալի բանաձևը.
Ավանդույթի համաձայն, եկեք ֆակտորիզացնենք համարիչը, սա մեծապես կպարզեցնի պատասխանը.
Բարդ ֆունկցիան պարտադիր չէ, որ կես կիլոմետր երկարությամբ բանաձև լինի: Օրինակ, բավական է վերցնել ֆունկցիան զ(x) = մեղք xև փոխարինել փոփոխականը x, ասենք, վրա x 2 + ln x. Կստացվի զ(x) = մեղք ( x 2 + ln x) - սա բարդ գործառույթ է: Այն ունի նաև ածանցյալ, բայց այն հնարավոր չի լինի գտնել՝ օգտագործելով վերը քննարկված կանոնները։
Ինչ պետք է անեմ? Նման դեպքերում բարդ ֆունկցիայի ածանցյալի փոփոխականի և բանաձևի փոխարինումը օգնում է.
զ ’(x) = զ ’(տ) · տ», Եթե xփոխարինվում է տ(x).
Որպես կանոն, այս բանաձևը հասկանալու հետ կապված իրավիճակը նույնիսկ ավելի տխուր է, քան գործակիցի ածանցյալը: Ուստի ավելի լավ է նաև դա բացատրել կոնկրետ օրինակներով, հետ մանրամասն նկարագրությունամեն քայլափոխի.
Առաջադրանք. Գտեք ֆունկցիաների ածանցյալները. զ(x) = ե 2x + 3 ; է(x) = մեղք ( x 2 + ln x)
Նշենք, որ եթե ֆունկցիայի մեջ զ(x) 2 արտահայտության փոխարեն x+ 3 հեշտ կլինի x, ապա ստանում ենք տարրական ֆունկցիա զ(x) = ե x. Հետևաբար, մենք կատարում ենք փոխարինում. թող 2 x + 3 = տ, զ(x) = զ(տ) = ե տ. Մենք փնտրում ենք բարդ ֆունկցիայի ածանցյալ՝ օգտագործելով բանաձևը.
զ ’(x) = զ ’(տ) · տ ’ = (ե տ)’ · տ ’ = ե տ · տ ’
Եվ հիմա - ուշադրություն: Մենք կատարում ենք հակադարձ փոխարինում. տ = 2x+ 3. Մենք ստանում ենք.
զ ’(x) = ե տ · տ ’ = ե 2x+ 3 (2 x + 3)’ = ե 2x+ 3 2 = 2 ե 2x + 3
Հիմա եկեք նայենք ֆունկցիային է(x). Ակնհայտ է, որ այն պետք է փոխարինվի x 2 + ln x = տ. Մենք ունենք:
է ’(x) = է ’(տ) · տ= (մեղ տ)’ · տ= cos տ · տ ’
Հակադարձ փոխարինում. տ = x 2 + ln x. Ապա.
է ’(x) = cos ( x 2 + ln x) · ( x 2 + ln x)’ = cos ( x 2 + ln x) · (2 x + 1/x).
Այսքանը: Ինչպես երևում է վերջին արտահայտությունից, ամբողջ խնդիրը կրճատվել է մինչև ածանցյալ գումարի հաշվարկը։
Պատասխան.
զ ’(x) = 2 · ե
2x + 3 ;
է ’(x) = (2x + 1/x) cos ( x 2 + ln x).
Շատ հաճախ իմ դասերի ժամանակ «ածանցյալ» տերմինի փոխարեն ես օգտագործում եմ «պրիմ» բառը։ Օրինակ, գումարի հարվածը հավասար է հարվածների գումարին: Դա ավելի պարզ է? Դե, դա լավ է:
Այսպիսով, ածանցյալի հաշվարկը հանգում է վերը քննարկված կանոնների համաձայն այս նույն հարվածներից ազատվելուն: Որպես վերջնական օրինակ՝ վերադառնանք ռացիոնալ ցուցիչով ածանցյալ հզորությանը.
(x n)’ = n · x n − 1
Քչերը գիտեն դա դերում nկարող է լինել կոտորակային թիվ: Օրինակ, արմատն է x 0.5. Իսկ եթե արմատի տակ ինչ-որ շքեղ բան կա: Դարձյալ արդյունքը կլինի բարդ ֆունկցիա՝ նրանք սիրում են նման կոնստրուկցիաներ տալ թեստերև քննություններ։
Առաջադրանք. Գտեք ֆունկցիայի ածանցյալը.
Նախ, եկեք արմատը վերագրենք որպես ռացիոնալ ցուցիչ ունեցող ուժ.
զ(x) = (x 2 + 8x − 7) 0,5 .
Այժմ մենք փոխարինում ենք. թող x 2 + 8x − 7 = տ. Մենք գտնում ենք ածանցյալը բանաձևով.
զ ’(x) = զ ’(տ) · տ ’ = (տ 0.5)» · տ= 0,5 · տ−0,5 · տ ’.
Եկեք կատարենք հակառակ փոխարինումը. տ = x 2 + 8x− 7. Մենք ունենք.
զ ’(x) = 0,5 · ( x 2 + 8x− 7) −0,5 · ( x 2 + 8x− 7)’ = 0,5 (2 x+ 8) ( x 2 + 8x − 7) −0,5 .
Վերջապես, վերադառնանք արմատներին.
Այս դասը նվիրված է «Բարդ ֆունկցիաների տարբերակում. Խնդիր մաթեմատիկայի պետական միասնական քննությանը նախապատրաստվելու պրակտիկայից»։ Այս դասը ուսումնասիրում է բարդ ֆունկցիաների տարբերակումը: Կազմվում է բարդ ֆունկցիայի ածանցյալների աղյուսակ։ Բացի այդ, դիտարկվում է մաթեմատիկայի պետական միասնական քննությանը նախապատրաստվելու պրակտիկայից խնդրի լուծման օրինակ։
Թեմա՝ Ածանցյալ
Դաս. Բարդ ֆունկցիայի տարբերակում: Մաթեմատիկայի միասնական պետական քննությանը նախապատրաստվելու պրակտիկ առաջադրանք
Համալիրֆունկցիանմենք արդեն տարբերակել ենք, բայց փաստարկը գծային ֆունկցիա էր, այսինքն՝ մենք գիտենք, թե ինչպես կարելի է տարբերակել ֆունկցիան: Օրինակ, ։ Այժմ, նույն կերպ, մենք կգտնենք բարդ ֆունկցիայի ածանցյալներ, որտեղ գծային ֆունկցիայի փոխարեն կարող է լինել մեկ այլ ֆունկցիա։
Սկսենք ֆունկցիայից
Այսպիսով, մենք գտանք սինուսի ածանցյալը բարդ ֆունկցիայից, որտեղ սինուսի արգումենտը քառակուսի ֆունկցիա էր:
Եթե Ձեզ անհրաժեշտ է գտնել ածանցյալի արժեքը կոնկրետ կետում, ապա այս կետը պետք է փոխարինվի հայտնաբերված ածանցյալով:
Այսպիսով, երկու օրինակով մենք տեսանք, թե ինչպես է գործում կանոնը տարբերակումհամալիր գործառույթները.
2. ![]()
3. ![]() . Հիշեցնենք, որ.
. Հիշեցնենք, որ.
7. ![]()
8. ![]() .
.
Այսպիսով, մենք այս փուլում կավարտենք բարդ ֆունկցիաների տարբերակման աղյուսակը։ Այնուհետև, իհարկե, այն էլ ավելի կընդհանրացվի, բայց հիմա անցնենք ածանցյալի կոնկրետ խնդիրներին:
Միասնական պետական քննությանը նախապատրաստվելու պրակտիկայում առաջարկվում են հետևյալ առաջադրանքները.
Գտեք ֆունկցիայի նվազագույնը ![]() .
.
ՕՁ: ![]() .
.
Գտնենք ածանցյալը։ Հիշեցնենք, որ ս. ![]() .
.
Ածանցյալը հավասարեցնենք զրոյի։ Dot - ներառված է ODZ-ում:
Գտնենք ածանցյալի հաստատուն նշանի միջակայքերը (ֆունկցիայի միապաղաղության միջակայքերը) (տե՛ս նկ. 1):

Բրինձ. 1. Ֆունկցիայի համար միապաղաղության միջակայքերը ![]() .
.
Եկեք նայենք մի կետ և պարզենք, թե արդյոք դա ծայրահեղ կետ է: Ծայրահեղության բավարար նշանն այն է, որ ածանցյալը փոխում է նշանը կետով անցնելիս: Այս դեպքում ածանցյալը փոխում է նշանը, ինչը նշանակում է, որ դա ծայրահեղ կետ է: Քանի որ ածանցյալը փոխում է նշանը «-»-ից «+», ապա սա նվազագույն կետն է: Գտնենք արժեքըգործառույթները նվազագույն կետում. Եկեք գծենք դիագրամ (տես նկ. 2):

Նկ.2. Ֆունկցիայի ծայրահեղություն ![]() .
.
Ինտերվալի վրա - ֆունկցիան նվազում է, միացված - ֆունկցիան մեծանում է, ծայրահեղ կետը եզակի է: Ֆունկցիան իր ամենափոքր արժեքը վերցնում է միայն կետում:
Դասի ընթացքում դիտարկեցինք բարդ ֆունկցիաների տարբերակումը, կազմեցինք աղյուսակ և դիտարկեցինք բարդ ֆունկցիայի տարբերակման կանոնները և օրինակ բերեցինք միասնական պետական քննությանը նախապատրաստվելու պրակտիկայից ածանցյալ օգտագործելու օրինակ։
1. Հանրահաշիվ և վերլուծության սկիզբ, դասարան 10 (երկու մասից): Ձեռնարկի համար ուսումնական հաստատություններ (պրոֆիլի մակարդակը) խմբ. Ա.Գ.Մորդկովիչ. - M.: Mnemosyne, 2009 թ.
2. Հանրահաշիվ և վերլուծության սկիզբ, դասարան 10 (երկու մասից): Խնդիրների գիրք ուսումնական հաստատությունների համար (պրոֆիլի մակարդակ), խմբ. Ա.Գ.Մորդկովիչ. - M.: Mnemosyne, 2007:
3. Վիլենկին Ն.Յա., Իվաշև-Մուսատով Օ.Ս., Շվարցբուրդ Ս.Ի. Հանրահաշիվ և հաշվարկ 10-րդ դասարանի համար ( ուսուցողականմաթեմատիկայի խորացված ուսումնասիրությամբ դպրոցների և դասարանների աշակերտների համար):-Մ.: Պրոսվեշչենիե, 1996 թ.
4. Գալիցկի Մ.Լ., Մոշկովիչ Մ.Մ., Շվարցբուրդ Ս.Ի. Հանրահաշվի և մաթեմատիկական վերլուծության խորը ուսումնասիրություն:-Մ.: Կրթություն, 1997 թ.
5. Մաթեմատիկայի խնդիրների ժողովածու բարձրագույն ուսումնական հաստատությունների դիմորդների համար (խմբ. Մ.Ի. Սքանավի - Մ.: Բարձրագույն դպրոց, 1992 թ.):
6. Մերզլյակ Ա.Գ., Պոլոնսկի Վ.Բ., Յակիր Մ.Ս. Հանրահաշվական սիմուլյատոր.-K.: A.S.K., 1997 թ.
7. Զվավիչ Լ.Ի., Շլյապոչնիկ Լ.Յա., Չինկինա հանրահաշիվը և վերլուծության սկիզբը: 8-11 դասարաններ՝ մաթեմատիկայի խորացված ուսումնասիրությամբ ձեռնարկ դպրոցների և դասարանների համար - Մ.: Բուստարդ, 2002 թ.
8. Սահակյան Ս.Մ., Գոլդման Ա.Մ., Դենիսով Դ.Վ. Խնդիրներ հանրահաշվի և վերլուծության սկզբունքների վերաբերյալ (ձեռնարկ հանրակրթական հաստատությունների 10-11-րդ դասարանների աշակերտների համար - Մ.: Prosveshchenie, 2003 թ.):
9. Կարպ Ա.Պ. Հանրահաշվի խնդիրների և վերլուծության սկզբունքների ժողովածու. Դասագիրք. նպաստ 10-11 դասարանների համար. խորությամբ ուսումնասիրված Մաթեմատիկա.-Մ.՝ Կրթություն, 2006 թ.
10. Գլեյզեր Գ.Ի. Մաթեմատիկայի պատմությունը դպրոցում. 9-10 դասարաններ (ձեռնարկ ուսուցիչների համար):-Մ.: Կրթություն, 1983 թ
Լրացուցիչ վեբ ռեսուրսներ
2. Բնական գիտությունների պորտալ ().
Պատրաստեք այն տանը
Թիվ 42.2, 42.3 (Հանրահաշիվ և վերլուծության սկիզբ, 10-րդ դասարան (երկու մասով): Խնդիրների գիրք հանրակրթական հաստատությունների համար (պրոֆիլի մակարդակ) խմբագրել է Ա. Գ. Մորդկովիչը: - Մ.: Mnemosyne, 2007 թ.
Որի վրա մենք ուսումնասիրեցինք ամենապարզ ածանցյալները, ինչպես նաև ծանոթացանք տարբերակման կանոններին և ածանցյալներ գտնելու որոշ տեխնիկական մեթոդներին: Այսպիսով, եթե դուք այնքան էլ լավ չեք տիրապետում ֆունկցիաների ածանցյալներին կամ եթե այս հոդվածի որոշ կետեր լիովին պարզ չեն, ապա նախ կարդացեք վերը նշված դասը: Խնդրում եմ լուրջ տրամադրություն ձեռք բերեք՝ նյութը պարզ չէ, բայց ես դեռ կփորձեմ ներկայացնել այն պարզ և հստակ։
Գործնականում բարդ ֆունկցիայի ածանցյալի հետ պետք է շատ հաճախ, ես կասեի, գրեթե միշտ, երբ քեզ առաջադրանքներ են տալիս գտնել ածանցյալներ։
Մենք նայում ենք աղյուսակին (թիվ 5) բարդ ֆունկցիան տարբերակելու կանոնին.
Եկեք պարզենք այն: Առաջին հերթին ուշադրություն դարձնենք մուտքին. Այստեղ մենք ունենք երկու ֆունկցիա՝ և , և ֆունկցիան, պատկերավոր ասած, գտնվում է ֆունկցիայի ներսում: Այս տիպի ֆունկցիան (երբ մի ֆունկցիան տեղադրված է մյուսի մեջ) կոչվում է կոմպլեքս ֆունկցիա։
Ես կկանչեմ գործառույթը արտաքին ֆունկցիաև ֆունկցիան - ներքին (կամ ներդիր) ֆունկցիա.
! Այս սահմանումները տեսական չեն և չպետք է հայտնվեն առաջադրանքների վերջնական ձևավորման մեջ: Ես օգտագործում եմ «արտաքին գործառույթ», «ներքին» ոչ ֆորմալ արտահայտությունները միայն նյութը հասկանալու համար:
Իրավիճակը պարզաբանելու համար հաշվի առեք.
Օրինակ 1
Գտե՛ք ֆունկցիայի ածանցյալը
Սինուսի տակ մենք ունենք ոչ միայն «X» տառը, այլ մի ամբողջ արտահայտություն, ուստի աղյուսակից անմիջապես ածանցյալը գտնելը չի աշխատի: Մենք նաև նկատում ենք, որ այստեղ անհնար է կիրառել առաջին չորս կանոնները, թվում է, թե տարբերություն կա, բայց փաստն այն է, որ սինուսը չի կարող «կտոր լինել».
Այս օրինակում իմ բացատրություններից արդեն ինտուիտիվորեն պարզ է դառնում, որ ֆունկցիան բարդ ֆունկցիա է, իսկ բազմանդամը՝ ներքին ֆունկցիա (ներկառուցում) և արտաքին ֆունկցիա։
Առաջին քայլըայն, ինչ դուք պետք է անեք, երբ գտնեք բարդ ֆունկցիայի ածանցյալը հասկանալ, թե որ գործառույթն է ներքին և որը արտաքին.
Պարզ օրինակների դեպքում պարզ է թվում, որ սինուսի տակ բազմանդամ է տեղադրված։ Բայց ինչ անել, եթե ամեն ինչ ակնհայտ չէ: Ինչպե՞ս ճշգրիտ որոշել, թե որ գործառույթն է արտաքին և որը ներքին: Դա անելու համար առաջարկում եմ օգտագործել հետևյալ տեխնիկան, որը կարելի է անել մտովի կամ սևագրով։
Պատկերացնենք, որ հաշվիչի վրա պետք է հաշվարկել արտահայտության արժեքը (մեկի փոխարեն կարող է լինել ցանկացած թիվ)։
Ի՞նչ ենք մենք առաջինը հաշվարկելու: Նախ եւ առաջդուք պետք է կատարեք հետևյալ գործողությունը՝ , հետևաբար բազմանդամը կլինի ներքին ֆունկցիա. 
Երկրորդպետք է գտնել, ուստի սինուսը կլինի արտաքին ֆունկցիա. 
Մեզնից հետո ՎԱՃԱՌՎԱԾ Էներքին և արտաքին գործառույթներով ժամանակն է կիրառել բարդ ֆունկցիաների տարբերակման կանոնը ![]() .
.
Եկեք սկսենք որոշել. Դասից Ինչպե՞ս գտնել ածանցյալը:մենք հիշում ենք, որ ցանկացած ածանցյալի լուծման ձևավորումը միշտ սկսվում է այսպես.
![]()
Սկզբումգտնում ենք արտաքին ֆունկցիայի (սինուսի) ածանցյալը, նայում տարրական ֆունկցիաների ածանցյալների աղյուսակին և նկատում, որ . Բոլոր աղյուսակի բանաձևերը կիրառելի են նաև, եթե «x»-ը փոխարինվի բարդ արտահայտությամբ, այս դեպքում:
![]()
Խնդրում ենք նկատի ունենալ, որ ներքին գործառույթը չի փոխվել, մենք դրան չենք դիպչում.
Դե, դա միանգամայն ակնհայտ է
Բանաձևի կիրառման արդյունքը ![]() իր վերջնական տեսքով այն ունի հետևյալ տեսքը.
իր վերջնական տեսքով այն ունի հետևյալ տեսքը.
Մշտական գործոնը սովորաբար դրվում է արտահայտության սկզբում.
Եթե որևէ թյուրիմացություն կա, լուծումը գրեք թղթի վրա և նորից կարդացեք բացատրությունները:
Օրինակ 2
Գտե՛ք ֆունկցիայի ածանցյալը
Օրինակ 3
Գտե՛ք ֆունկցիայի ածանցյալը
Ինչպես միշտ, մենք գրում ենք. ![]()
Եկեք պարզենք, թե որտեղ ունենք արտաքին և որտեղ՝ ներքին: Դա անելու համար մենք փորձում ենք (մտավոր կամ սևագրով) հաշվարկել արտահայտության արժեքը . Ի՞նչ պետք է անեք առաջինը: Նախևառաջ պետք է հաշվարկել, թե ինչի է հավասար հիմքը. հետևաբար, բազմանդամը ներքին ֆունկցիան է. 
Եվ միայն դրանից հետո է կատարվում աստիճանավորումը, հետևաբար, հզորության ֆունկցիան արտաքին ֆունկցիա է. 
Ըստ բանաձևի ![]() , նախ պետք է գտնել արտաքին ֆունկցիայի ածանցյալը, այս դեպքում՝ աստիճանը։ Աղյուսակում փնտրում ենք պահանջվող բանաձևը. Կրկին կրկնում ենք. ցանկացած աղյուսակային բանաձև վավեր է ոչ միայն «X», այլև բարդ արտահայտության համար. Այսպիսով, բարդ ֆունկցիայի տարբերակման կանոնի կիրառման արդյունքը
, նախ պետք է գտնել արտաքին ֆունկցիայի ածանցյալը, այս դեպքում՝ աստիճանը։ Աղյուսակում փնտրում ենք պահանջվող բանաձևը. Կրկին կրկնում ենք. ցանկացած աղյուսակային բանաձև վավեր է ոչ միայն «X», այլև բարդ արտահայտության համար. Այսպիսով, բարդ ֆունկցիայի տարբերակման կանոնի կիրառման արդյունքը ![]() հաջորդը՝
հաջորդը՝
Կրկին շեշտում եմ, որ երբ վերցնում ենք արտաքին ֆունկցիայի ածանցյալը, մեր ներքին ֆունկցիան չի փոխվում. 
Այժմ մնում է միայն գտնել ներքին ֆունկցիայի շատ պարզ ածանցյալը և մի փոքր շտկել արդյունքը.

Օրինակ 4
Գտե՛ք ֆունկցիայի ածանցյալը
Սա օրինակ է անկախ որոշում(պատասխանեք դասի վերջում):
Բարդ ֆունկցիայի ածանցյալի մասին ձեր ըմբռնումը համախմբելու համար ես օրինակ կբերեմ առանց մեկնաբանությունների, փորձեք ինքնուրույն պարզել այն, պատճառաբանեք, թե որտեղ է արտաքին և որտեղ է ներքին գործառույթը, ինչու են առաջադրանքները լուծվում այսպես:
Օրինակ 5
ա) Գտե՛ք ֆունկցիայի ածանցյալը
բ) Գտե՛ք ֆունկցիայի ածանցյալը
Օրինակ 6
Գտե՛ք ֆունկցիայի ածանցյալը ![]()
Այստեղ մենք ունենք արմատ, և արմատը տարբերելու համար այն պետք է ներկայացվի որպես ուժ։ Այսպիսով, նախ մենք ֆունկցիան բերում ենք տարբերակման համար համապատասխան ձևի.

Վերլուծելով ֆունկցիան՝ գալիս ենք այն եզրակացության, որ երեք անդամների գումարը ներքին ֆունկցիա է, իսկ հզորության բարձրացումը՝ արտաքին ֆունկցիա։ Կիրառում ենք բարդ ֆունկցիաների տարբերակման կանոնը ![]() :
:

Մենք կրկին ներկայացնում ենք աստիճանը որպես ռադիկալ (արմատ), իսկ ներքին ֆունկցիայի ածանցյալի համար կիրառում ենք գումարը տարբերակելու պարզ կանոն.

Պատրաստ. Կարող եք նաև կրճատել արտահայտությունը փակագծերում ընդհանուր հայտարարի և ամեն ինչ գրել մեկ կոտորակի տեսքով: Դա, իհարկե, գեղեցիկ է, բայց երբ դուք ստանում եք ծանր երկար ածանցյալներ, ավելի լավ է դա չանել (հեշտ է շփոթվել, անհարկի սխալ թույլ տալ, և ուսուցչի համար անհարմար կլինի ստուգել):
Օրինակ 7
Գտե՛ք ֆունկցիայի ածանցյալը
Սա ձեզ համար ինքնուրույն լուծելու օրինակ է (պատասխանեք դասի վերջում):
Հետաքրքիր է նշել, որ երբեմն բարդ ֆունկցիան տարբերելու կանոնի փոխարեն կարող եք օգտագործել գործակիցը տարբերելու կանոնը.  , բայց նման լուծումը արտասովոր այլասերվածության տեսք կունենա։ Ահա տիպիկ օրինակ.
, բայց նման լուծումը արտասովոր այլասերվածության տեսք կունենա։ Ահա տիպիկ օրինակ.
Օրինակ 8
Գտե՛ք ֆունկցիայի ածանցյալը
Այստեղ դուք կարող եք օգտագործել գործակիցի տարբերակման կանոնը  , բայց շատ ավելի ձեռնտու է գտնել ածանցյալը բարդ ֆունկցիայի տարբերակման կանոնի միջոցով.
, բայց շատ ավելի ձեռնտու է գտնել ածանցյալը բարդ ֆունկցիայի տարբերակման կանոնի միջոցով.
Մենք ֆունկցիան պատրաստում ենք տարբերակման համար. մինուսը դուրս ենք հանում ածանցյալ նշանից և կոսինուսը բարձրացնում ենք համարիչի մեջ.

Կոսինուսը ներքին ֆունկցիա է, հզորացումը՝ արտաքին ֆունկցիա։
Եկեք օգտագործենք մեր կանոնը ![]() :
:

Մենք գտնում ենք ներքին ֆունկցիայի ածանցյալը և վերականգնում ենք կոսինուսը.

Պատրաստ. Դիտարկված օրինակում կարևոր է չշփոթվել նշանների մեջ: Ի դեպ, փորձեք լուծել այն՝ օգտագործելով կանոնը  , պատասխանները պետք է համընկնեն։
, պատասխանները պետք է համընկնեն։
Օրինակ 9
Գտե՛ք ֆունկցիայի ածանցյալը
Սա ձեզ համար ինքնուրույն լուծելու օրինակ է (պատասխանեք դասի վերջում):
Մինչ այժմ մենք դիտարկել ենք դեպքեր, երբ մենք ունեցել ենք միայն մեկ բույն՝ բարդ ֆունկցիայի մեջ: Գործնական առաջադրանքներում հաճախ կարելի է գտնել ածանցյալներ, որտեղ, ինչպես բնադրող տիկնիկները, մեկը մյուսի մեջ, միանգամից 3 կամ նույնիսկ 4-5 ֆունկցիա է դրված:
Օրինակ 10
Գտե՛ք ֆունկցիայի ածանցյալը
Եկեք հասկանանք այս ֆունկցիայի հավելվածները։ Փորձենք հաշվարկել արտահայտությունը՝ օգտագործելով փորձարարական արժեքը։ Ինչպե՞ս կարող ենք հաշվել հաշվիչի վրա:
Նախ պետք է գտնել, ինչը նշանակում է, որ արկսինը ամենախորը ներկառուցումն է.
Այնուհետև մեկի այս աղեղը պետք է քառակուսի լինի.
Եվ վերջապես, մենք յոթը բարձրացնում ենք ուժի. 
Այսինքն՝ այս օրինակում մենք ունենք երեք տարբեր ֆունկցիաներ և երկու ներկառուցումներ, մինչդեռ ամենաներքին ֆունկցիան աղեղն է, իսկ ամենաարտաքինը՝ էքսպոնենցիալ ֆունկցիան։
Եկեք սկսենք որոշել
Ըստ կանոնի ![]() Նախ պետք է վերցնել արտաքին ֆունկցիայի ածանցյալը: Մենք նայում ենք ածանցյալների աղյուսակին և գտնում ենք ածանցյալը էքսպոնենցիալ ֆունկցիաՄիակ տարբերությունն այն է, որ «x»-ի փոխարեն ունենք բարդ արտահայտություն, որը չի ժխտում այս բանաձեւի վավերականությունը։ Այսպիսով, բարդ ֆունկցիայի տարբերակման կանոնի կիրառման արդյունքը
Նախ պետք է վերցնել արտաքին ֆունկցիայի ածանցյալը: Մենք նայում ենք ածանցյալների աղյուսակին և գտնում ենք ածանցյալը էքսպոնենցիալ ֆունկցիաՄիակ տարբերությունն այն է, որ «x»-ի փոխարեն ունենք բարդ արտահայտություն, որը չի ժխտում այս բանաձեւի վավերականությունը։ Այսպիսով, բարդ ֆունկցիայի տարբերակման կանոնի կիրառման արդյունքը ![]() հաջորդ.
հաջորդ.
Գործառույթներ բարդ տեսակմիշտ չէ, որ համապատասխանում են բարդ ֆունկցիայի սահմանմանը: Եթե կա y = sin x - (2 - 3) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11 ձևի ֆունկցիա, ապա այն չի կարող բարդ համարվել, ի տարբերություն y = sin 2 x:
Այս հոդվածը ցույց կտա բարդ ֆունկցիայի հայեցակարգը և դրա նույնականացումը: Եզրակացության մեջ լուծումների օրինակներով աշխատենք ածանցյալը գտնելու բանաձևերով։ Ածանցյալ աղյուսակի և տարբերակման կանոնների օգտագործումը զգալիորեն նվազեցնում է ածանցյալը գտնելու ժամանակը:
Հիմնական սահմանումներ
Սահմանում 1Կոմպլեքս ֆունկցիան այն ֆունկցիան է, որի փաստարկը նույնպես ֆունկցիա է:
Այն նշվում է այսպես՝ f (g (x)): Ունենք, որ g (x) ֆունկցիան համարվում է f արգումենտ (g (x)):
Սահմանում 2
Եթե կա f ֆունկցիա և այն կոտանգենս ֆունկցիա է, ապա g(x) = ln x բնական լոգարիթմի ֆունկցիան է։ Մենք գտնում ենք, որ f (g (x)) կոմպլեքս ֆունկցիան կգրվի arctg(lnx): Կամ f ֆունկցիան, որը 4-րդ աստիճանի բարձրացված ֆունկցիա է, որտեղ g (x) = x 2 + 2 x - 3 համարվում է ամբողջ ռացիոնալ ֆունկցիա, մենք ստանում ենք, որ f (g (x)) = (x 2 + 2 x - 3) 4.
Ակնհայտ է, որ g(x)-ը կարող է բարդ լինել: y = sin 2 x + 1 x 3 - 5 օրինակից պարզ է դառնում, որ g-ի արժեքն ունի կոտորակի խորանարդային արմատը։ Այս արտահայտությունը կարող է նշանակվել որպես y = f (f 1 (f 2 (x))): Այնտեղից մենք ունենք, որ f-ը սինուսային ֆունկցիա է, իսկ f 1-ը քառակուսի արմատի տակ գտնվող ֆունկցիա է, f 2 (x) = 2 x + 1 x 3 - 5-ը կոտորակային ռացիոնալ ֆունկցիա է:
Սահմանում 3
Բնադրման աստիճանը որոշվում է ցանկացած բնական թիվև գրվում է որպես y = f (f 1 (f 2 (f 3 (... (f n (x)))))) .
Սահմանում 4
Ֆունկցիայի կազմության հայեցակարգը վերաբերում է ներդիր ֆունկցիաների քանակին՝ ըստ խնդրի պայմանների։ Լուծելու համար օգտագործեք ձևի բարդ ֆունկցիայի ածանցյալը գտնելու բանաձևը
(f (g (x))) " = f " (g (x)) g " (x)
Օրինակներ
Օրինակ 1Գտե՛ք y = (2 x + 1) ձևի բարդ ֆունկցիայի ածանցյալը 2.
Լուծում
Պայմանը ցույց է տալիս, որ f-ը քառակուսի ֆունկցիա է, իսկ g(x) = 2 x + 1 համարվում է գծային ֆունկցիա:
Կիրառենք բարդ ֆունկցիայի ածանցյալ բանաձևը և գրենք.
f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 գ (x) = 2 (2 x + 1); g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f « (g (x)) g» (x) = 2 (2 x + 1) 2 = 8 x + 4
Անհրաժեշտ է գտնել ածանցյալ ֆունկցիայի պարզեցված սկզբնական ձևով։ Մենք ստանում ենք.
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
Այստեղից մենք ունենք դա
y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4
Արդյունքները նույնն էին.
Այս տեսակի խնդիրներ լուծելիս կարևոր է հասկանալ, թե որտեղ է գտնվելու f և g (x) ձևի ֆունկցիան։
Օրինակ 2
Դուք պետք է գտնեք y = sin 2 x և y = sin x 2 ձևի բարդ ֆունկցիաների ածանցյալները:
Լուծում
Ֆունկցիայի առաջին նշումն ասում է, որ f-ը քառակուսի ֆունկցիան է, իսկ g(x)-ը սինուսային ֆունկցիան է: Հետո մենք ստանում ենք դա
y " = (մեղք 2 x) " = 2 մեղք 2 - 1 x (մեղք x) " = 2 մեղք x cos x
Երկրորդ մուտքը ցույց է տալիս, որ f-ը սինուսային ֆունկցիա է, իսկ g(x) = x 2-ը նշանակում է հզորության ֆունկցիա: Հետևում է, որ բարդ ֆունկցիայի արտադրյալը գրում ենք որպես
y " = (sin x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)
y = f (f 1 (f 2 (f 3 (. . . (f n (x))))) ածանցյալի բանաձևը կգրվի որպես y " = f " (f 1 (f 2 (f 3 (. (f n (x)))) · f 1 "(f 2 (f 3 (. )) )) · . . . fn «(x)
Օրինակ 3
Գտե՛ք y = sin ֆունկցիայի ածանցյալը (ln 3 a r c t g (2 x)):
Լուծում
Այս օրինակը ցույց է տալիս գրելու և ֆունկցիաների գտնվելու վայրը որոշելու դժվարությունը: Այնուհետև y = f (f 1 (f 2 (f 3 (f 4 (x))))) նշանակեք, որտեղ f , f 1 , f 2 , f 3 , f 4 (x) սինուսային ֆունկցիան է, բարձրացնելու ֆունկցիան։ մինչև 3 աստիճան, ֆունկցիա լոգարիթմով և հիմքով e, արկտանգենս և գծային ֆունկցիա:
Բարդ ֆունկցիա սահմանելու բանաձևից ունենք, որ
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x)) f 3 "(f 4 (x)) f 4" (x)
Մենք ստանում ենք այն, ինչ մենք պետք է գտնենք
- f "(f 1 (f 2 (f 3 (f 4 (x)))))) որպես սինուսի ածանցյալ ըստ ածանցյալների աղյուսակի, ապա f" (f 1 (f 2 (f 3 (f 4 ( x)))) = cos (ln 3 a r c t g (2 x)) .
- f 1 "(f 2 (f 3 (f 4 (x)))) որպես հզորության ֆունկցիայի ածանցյալ, ապա f 1" (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
- f 2" (f 3 (f 4 (x))) որպես լոգարիթմական ածանցյալ, ապա f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 "(f 4 (x)) որպես արկտանգենսի ածանցյալ, ապա f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2:
- f 4 (x) = 2 x ածանցյալը գտնելիս ածանցյալի նշանից հանեք 2-ը՝ օգտագործելով 1-ի հավասար ցուցիչ ունեցող հզորության ֆունկցիայի ածանցյալի բանաձևը, այնուհետև f 4" (x) = (2 x) «= 2 x» = 2 · 1 · x 1 - 1 = 2:
Մենք համատեղում ենք միջանկյալ արդյունքները և ստանում ենք դա
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x)) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)
Նման գործառույթների վերլուծությունը հիշեցնում է բնադրող տիկնիկների մասին: Տարբերակման կանոնները միշտ չեն կարող բացահայտորեն կիրառվել՝ օգտագործելով ածանցյալ աղյուսակը: Հաճախ անհրաժեշտ է օգտագործել բարդ ֆունկցիաների ածանցյալներ գտնելու բանաձև:
Բարդ տեսքի և բարդ գործառույթների միջև կան որոշ տարբերություններ: Սա տարբերելու հստակ ունակությամբ, ածանցյալներ գտնելը հատկապես հեշտ կլինի:
Օրինակ 4
Պետք է մտածել նման օրինակ բերելու մասին։ Եթե կա y = t g 2 x + 3 t g x + 1 ձևի ֆունկցիա, ապա այն կարելի է համարել g (x) = t g x, f (g) = g 2 + 3 g + 1 ձևի բարդ ֆունկցիա. . Ակնհայտ է, որ անհրաժեշտ է օգտագործել բարդ ածանցյալի բանաձևը.
f " (g (x)) = (g 2 (x) + 3 g (x) + 1) " = (g 2 (x)) " + (3 գ (x)) " + 1 " = = 2 · g 2 - 1 (x) + 3 գ »(x) + 0 = 2 գ (x) + 3 1 գ 1 - 1 (x) = = 2 գ (x) + 3 = 2 տ գ x + 3; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tg x + 3) · 1 cos 2 x = 2 t g x + 3 cos 2 x
y = t g x 2 + 3 t g x + 1 ձևի ֆունկցիան բարդ չի համարվում, քանի որ այն ունի tg x 2, 3 tg x և 1 գումարը: Այնուամենայնիվ, t g x 2-ը համարվում է բարդ ֆունկցիա, ապա մենք ստանում ենք g (x) = x 2 և f ձևի ուժային ֆունկցիա, որը շոշափող ֆունկցիա է: Դա անելու համար տարբերակեք ըստ քանակի: Մենք դա հասկանում ենք
y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x
Եկեք անցնենք բարդ ֆունկցիայի ածանցյալը գտնելուն (t g x 2) ":
f "(g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)
Մենք ստանում ենք, որ y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Կոմպլեքս տիպի ֆունկցիաները կարող են ներառվել բարդ ֆունկցիաների մեջ, իսկ բարդ ֆունկցիաները կարող են լինել բարդ տիպի ֆունկցիաների բաղադրիչներ։
Օրինակ 5
Օրինակ, դիտարկենք y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) ձևի բարդ ֆունկցիա:
Այս ֆունկցիան կարող է ներկայացվել որպես y = f (g (x)), որտեղ f-ի արժեքը 3-րդ բազային լոգարիթմի ֆունկցիա է, իսկ g (x)-ը համարվում է h (x) = ձևի երկու ֆունկցիաների գումարը: x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 և k (x) = ln 2 x · (x 2 + 1) . Ակնհայտորեն, y = f (h (x) + k (x)):
Դիտարկենք h(x) ֆունկցիան։ Սա հարաբերակցությունն է l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 դեպի m (x) = e x 2 + 3 3
Մենք ունենք, որ l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) երկու ֆունկցիաների գումարն է n (x) = x 2 + 7 և p ( x) = 3 cos 3 (2 x + 1) , որտեղ p (x) = 3 p 1 (p 2 (p 3 (x))) 3 թվային գործակցով բարդ ֆունկցիա է, իսկ p 1-ը խորանարդի ֆունկցիա է, p 2 ըստ կոսինուսի ֆունկցիայի, p 3 (x) = 2 x + 1 գծային ֆունկցիայի կողմից:
Մենք գտանք, որ m (x) = e x 2 + 3 3 = q (x) + r (x) երկու ֆունկցիաների գումարն է q (x) = e x 2 և r (x) = 3 3, որտեղ q (x) = q 1 (q 2 (x)) բարդ ֆունկցիա է, q 1-ը էքսպոնենցիալով ֆունկցիա է, q 2 (x) = x 2-ը հզորության ֆունկցիա է։
Սա ցույց է տալիս, որ h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)
Երբ անցնում ենք k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) ձևի արտահայտությանը, պարզ է, որ գործառույթը ներկայացված է բարդ s (-ի տեսքով. x) = ln 2 x = s 1 ( s 2 (x)) ռացիոնալ ամբողջ թվով t (x) = x 2 + 1, որտեղ s 1-ը քառակուսի ֆունկցիա է, իսկ s 2 (x) = ln x-ը լոգարիթմական է: հիմք էլ.
Հետևում է, որ արտահայտությունը կունենա k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x) ձևը:
Հետո մենք ստանում ենք դա
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)
Ելնելով ֆունկցիայի կառուցվածքներից՝ պարզ դարձավ, թե ինչպես և ինչ բանաձևեր է պետք օգտագործել արտահայտությունը տարբերակելիս պարզեցնելու համար։ Նման խնդիրներին ծանոթանալու և դրանց լուծման հայեցակարգին ծանոթանալու համար անհրաժեշտ է դիմել ֆունկցիայի տարբերակման, այսինքն՝ դրա ածանցյալը գտնելու կետին։
Եթե տեքստում սխալ եք նկատում, ընդգծեք այն և սեղմեք Ctrl+Enter