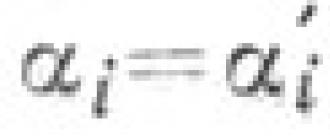17 ներդաշնակ թրթռումների հավասարում և գրաֆիկներ: Հարմոնիկ տատանումների հավասարումը և դրա նշանակությունը տատանողական պրոցեսների բնույթի ուսումնասիրության մեջ։ Խոնավացված տատանումների ժամանակաշրջան Տ

Պետական ​​միասնական քննության կոդավորիչի թեմաներ. ներդաշնակ թրթռումներ; տատանումների լայնություն, ժամանակաշրջան, հաճախականություն, փուլ; ազատ թրթռումներ, հարկադիր թրթռումներ, ռեզոնանս:

Տատանումներ -Դրանք համակարգի վիճակի փոփոխություններ են, որոնք ժամանակի ընթացքում կրկնվում են։ Տատանումներ հասկացությունն ընդգրկում է երևույթների շատ լայն շրջանակ։

մեխանիկական համակարգերի թրթռումներ, կամ մեխանիկական թրթռումներ- Սա մեխանիկական շարժումմարմին կամ մարմինների համակարգ, որը ժամանակի ընթացքում կրկնվող է և տեղի է ունենում հավասարակշռության դիրքի մոտակայքում։ Հավասարակշռության դիրքըհամակարգի վիճակ է, որտեղ այն կարող է մնալ անորոշ ժամանակով` առանց արտաքին ազդեցությունների:

Օրինակ, եթե ճոճանակը շեղվի և ազատ արձակվի, այն կսկսի տատանվել: Հավասարակշռության դիրքը ճոճանակի դիրքն է շեղման բացակայության դեպքում: Ճոճանակը, եթե չխանգարվի, կարող է մնալ այս դիրքում այնքան ժամանակ, որքան ցանկանում եք: Երբ ճոճանակը տատանվում է, այն բազմիցս անցնում է իր հավասարակշռության դիրքով։

Շեղված ճոճանակը բաց թողնելուց անմիջապես հետո այն սկսեց շարժվել, անցավ հավասարակշռության դիրքը, հասավ հակառակ ծայրահեղ դիրքի, մի պահ կանգ առավ այնտեղ և շարժվեց դեպի. հակադարձ ուղղություն, կրկին անցավ հավասարակշռության դիրքը և հետ վերադարձավ։ Մի բան է պատահել ամբողջ թափով. Այնուհետև այս գործընթացը պարբերաբար կկրկնվի։

Մարմնի տատանումների ամպլիտուդ հավասարակշռության դիրքից նրա ամենամեծ շեղման մեծությունն է։

Տատանումների ժամանակաշրջան - սա մեկ ամբողջական տատանման ժամանակն է: Կարելի է ասել, որ ժամանակաշրջանի ընթացքում մարմինը անցնում է չորս ամպլիտուդների ճանապարհ։

Տատանումների հաճախականությունը ժամանակաշրջանի փոխադարձ է. Հաճախականությունը չափվում է Հերցով (Հց) և ցույց է տալիս, թե քանի ամբողջական տատանումներ են տեղի ունենում մեկ վայրկյանում։

Հարմոնիկ թրթռումներ.

Մենք կենթադրենք, որ տատանվող մարմնի դիրքը որոշվում է մեկ կոորդինատով։ Հավասարակշռության դիրքը համապատասխանում է արժեքին. Մեխանիկայի հիմնական խնդիրն այս դեպքում ցանկացած պահի մարմնի կոորդինատը տվող ֆունկցիա գտնելն է։

Տատանումների մաթեմատիկական նկարագրության համար բնական է օգտագործել պարբերական ֆունկցիաներ։ Նման գործառույթները շատ են, բայց դրանցից երկուսը` սինուսը և կոսինուսը, ամենակարևորն են: Նրանք ունեն շատ լավ հատկություններ և սերտորեն կապված են ֆիզիկական երևույթների լայն շրջանակի հետ։

Քանի որ սինուսի և կոսինուսի ֆունկցիաները ստացվում են միմյանցից՝ արգումենտը տեղափոխելով , մենք կարող ենք սահմանափակվել դրանցից միայն մեկով: Որոշակիության համար մենք կօգտագործենք կոսինուս:

Հարմոնիկ թրթռումներ- սրանք տատանումներ են, որոնցում կոորդինատը կախված է ժամանակից՝ ներդաշնակ օրենքի համաձայն.

(1)

Եկեք պարզենք այս բանաձևում ներառված քանակությունների նշանակությունը։

Դրական արժեքը կոորդինատի ամենամեծ մոդուլի արժեքն է (քանի որ կոսինուսի մոդուլի առավելագույն արժեքը հավասար է միասնության), այսինքն՝ հավասարակշռության դիրքից ամենամեծ շեղումը։ Հետեւաբար - տատանումների ամպլիտուդը:

Կոսինուսի փաստարկը կոչվում է փուլերկմտանք. Ֆազային արժեքին հավասար արժեքը կոչվում է սկզբնական փուլ: Սկզբնական փուլը համապատասխանում է մարմնի սկզբնական կոորդինատին.

Քանակը կոչվում է ցիկլային հաճախականություն. Գտնենք դրա կապը տատանումների ժամանակաշրջանի և հաճախականության հետ։ Մեկ ամբողջական տատանումը համապատասխանում է ռադիանի հավասար փուլային աճին

(2)

(3)

Ցիկլային հաճախականությունը չափվում է ռադ/վ-ով (ռադիան/վրկ):

Համաձայն (2) և (3) արտահայտությունների, մենք ստանում ենք հարմոնիկ օրենքը գրելու ևս երկու ձև (1).

Հարմոնիկ տատանումների ժամանակ կոորդինատի կախվածությունը ժամանակից արտահայտող ֆունկցիայի գրաֆիկը (1) ներկայացված է Նկ. 1 .

(1) տիպի ներդաշնակ օրենքը ամենաընդհանուր բնույթ է կրում։ Այն արձագանքում է, օրինակ, իրավիճակներին, երբ ճոճանակի վրա միաժամանակ երկու սկզբնական գործողություն է կատարվել. այն շեղվել է որոշակի քանակությամբ և տրվել է որոշակի սկզբնական արագություն: Կան երկու կարևոր հատուկ դեպքեր, երբ այդ գործողություններից մեկը չի կատարվել.

Թող ճոճանակը շեղվի, բայց սկզբնական արագությունը չի հաղորդվել (այն բաց է թողնվել առանց նախնական արագության): Հասկանալի է , որ այս դեպքում , հետեւաբար կարող ենք դնել . Մենք ստանում ենք կոսինուսի օրենքը.

Հարմոնիկ տատանումների գրաֆիկն այս դեպքում ներկայացված է Նկ. 2.

Բրինձ. 2. Կոսինուսի օրենք

Այժմ ենթադրենք, որ ճոճանակը չի շեղվել, բայց հավասարակշռության դիրքից սկզբնական արագությունը նրան փոխանցվել է հարվածի միջոցով: Այս դեպքում, այնպես որ կարող եք տեղադրել . Մենք ստանում ենք սինուսի օրենքը.

Տատանումների գրաֆիկը ներկայացված է Նկ. 3.

Բրինձ. 3. Սինուսի օրենքը

Հարմոնիկ թրթռումների հավասարումը.

Վերադառնանք ընդհանուր հարմոնիկ օրենքին (1): Տարբերակենք այս հավասարությունը.

. (4)

Այժմ մենք տարբերակում ենք ստացված հավասարությունը (4).

. (5)

Եկեք համեմատենք (1) արտահայտությունը կոորդինատի համար և (5) արտահայտությունը արագացման պրոյեկցիայի համար: Մենք տեսնում ենք, որ արագացման պրոյեկցիան կոորդինատից տարբերվում է միայն գործակցով.

. (6)

Այս հարաբերակցությունը կոչվում է ներդաշնակ հավասարում. Այն կարող է նաև վերաշարադրվել այս ձևով.

. (7)

Մաթեմատիկական տեսանկյունից հավասարումը (7) է դիֆերենցիալ հավասարում. Դիֆերենցիալ հավասարումների լուծումները ֆունկցիաներ են (ոչ թվեր, ինչպես սովորական հանրահաշիվում):
Այսպիսով, կարելի է ապացուցել, որ.

(7) հավասարման լուծումը (1) ձևի ցանկացած ֆունկցիա կամայական ;

Ոչ մի այլ ֆունկցիա այս հավասարման լուծում չէ:

Այլ կերպ ասած, հարաբերությունները (6), (7) նկարագրում են ներդաշնակ տատանումները ցիկլային հաճախականությամբ և միայն դրանք: Նախնական պայմաններից որոշվում են երկու հաստատուններ՝ կոորդինատների և արագության սկզբնական արժեքներից:

Գարնանային ճոճանակ.

Գարնանային ճոճանակ զսպանակին ամրացված բեռ է, որը կարող է տատանվել հորիզոնական կամ ուղղահայաց ուղղությամբ։

Գտնենք զսպանակային ճոճանակի փոքր հորիզոնական տատանումների ժամանակաշրջանը (նկ. 4): Տատանումները փոքր կլինեն, եթե աղբյուրի դեֆորմացիայի չափը շատ ավելի քիչ լինի, քան դրա չափսերը։ Փոքր դեֆորմացիաների համար մենք կարող ենք օգտագործել Հուկի օրենքը. Սա կհանգեցնի նրան, որ տատանումները ներդաշնակ են:

Մենք անտեսում ենք շփումը: Բեռը ունի զանգված, իսկ զսպանակի կոշտությունը հավասար է .

Կոորդինատը համապատասխանում է հավասարակշռության դիրքին, որտեղ զսպանակը դեֆորմացված չէ։ Հետևաբար, զսպանակի դեֆորմացիայի մեծությունը հավասար է բեռի կոորդինատների մոդուլին։

Բրինձ. 4. Գարնանային ճոճանակ

Հորիզոնական ուղղությամբ բեռի վրա գործում է միայն զսպանակից եկող առաձգական ուժը: Նյուտոնի երկրորդ օրենքը առանցքի վրա նախագծված բեռի համար ունի հետևյալ ձևը.

. (8)

Եթե ​​(բեռը տեղափոխվում է աջ, ինչպես նկարում), ապա առաձգական ուժն ուղղված է հակառակ ուղղությամբ, և . Եվ հակառակը, եթե, ապա. Նշանները և միշտ հակառակ են, ուստի Հուկի օրենքը կարելի է գրել հետևյալ կերպ.

Այնուհետև (8) հարաբերությունը ստանում է ձև.

Մենք ստացել ենք (6) ձևի ներդաշնակ տատանումների հավասարումը, որում

Այսպիսով, զսպանակային ճոճանակի տատանումների ցիկլային հաճախականությունը հավասար է.

. (9)

Այստեղից և հարաբերություններից մենք գտնում ենք զսպանակային ճոճանակի հորիզոնական տատանումների ժամանակաշրջանը.

. (10)

Եթե ​​դուք բեռ եք կախում զսպանակի վրա, ապա դուք ստանում եք զսպանակավոր ճոճանակ, որը տատանվում է ուղղահայաց ուղղությամբ: Կարելի է ցույց տալ, որ այս դեպքում բանաձևը (10) վավեր է տատանումների ժամանակաշրջանի համար:

Մաթեմատիկական ճոճանակ.

Մաթեմատիկական ճոճանակ փոքր մարմին է, որը կախված է անկշռելի, չընդլայնվող թելի վրա (նկ. 5): Մաթեմատիկական ճոճանակը կարող է տատանվել ուղղահայաց հարթության վրա՝ ձգողության դաշտում։

Բրինձ. 5. Մաթեմատիկական ճոճանակ

Գտնենք մաթեմատիկական ճոճանակի փոքր տատանումների պարբերությունը։ Թելի երկարությունը . Մենք անտեսում ենք օդի դիմադրությունը:

Եկեք գրենք Նյուտոնի երկրորդ օրենքը ճոճանակի համար.

և նախագծել այն առանցքի վրա.

Եթե ​​ճոճանակը վերցնում է այնպիսի դիրք, ինչպիսին նկարում է (այսինքն), ապա.

Եթե ​​ճոճանակը գտնվում է հավասարակշռության դիրքի մյուս կողմում (այսինքն), ապա.

Այսպիսով, ճոճանակի ցանկացած դիրքի համար մենք ունենք.

. (11)

Երբ ճոճանակը հանգստանում է հավասարակշռության դիրքում, հավասարությունը բավարարվում է: Փոքր տատանումների դեպքում, երբ ճոճանակի շեղումները հավասարակշռության դիրքից փոքր են (համեմատ թելի երկարության հետ), բավարարվում է մոտավոր հավասարությունը։ Եկեք օգտագործենք այն բանաձևում (11).

Սա (6) ձևի ներդաշնակ տատանումների հավասարումն է, որում

Հետևաբար, մաթեմատիկական ճոճանակի տատանումների ցիկլային հաճախականությունը հավասար է.

. (12)

Այսպիսով, մաթեմատիկական ճոճանակի տատանումների ժամանակաշրջանը.

. (13)

Խնդրում ենք նկատի ունենալ, որ բանաձևը (13) չի ներառում բեռի զանգվածը: Ի տարբերություն զսպանակային ճոճանակի, մաթեմատիկական ճոճանակի տատանումների ժամանակաշրջանը կախված չէ դրա զանգվածից։

Ազատ և հարկադիր թրթռումներ:

Ասում են՝ համակարգը անում է անվճար թրթռումներ, եթե այն մեկ անգամ հանվել է հավասարակշռության դիրքից և հետագայում թողնել ինքն իրեն։ Պարբերական արտաքին չկա
Այս դեպքում համակարգը որևէ ազդեցություն չի ունենում, և չկան էներգիայի ներքին աղբյուրներ, որոնք ապահովում են համակարգում տատանումները:

Վերևում քննարկված զսպանակի և մաթեմատիկական ճոճանակների տատանումները ազատ տատանումների օրինակներ են։

Այն հաճախականությունը, որով տեղի են ունենում ազատ թրթռումներ, կոչվում է բնական հաճախականությունտատանողական համակարգ. Այսպիսով, (9) և (12) բանաձևերը տալիս են զսպանակի և մաթեմատիկական ճոճանակների տատանումների բնական (ցիկլային) հաճախականությունները։

Իդեալականացված իրավիճակում շփման բացակայության դեպքում ազատ տատանումները անխափան են, այսինքն՝ ունեն հաստատուն ամպլիտուդ և տևում են անորոշ ժամանակով։ Իրական տատանողական համակարգերում շփումը միշտ առկա է, ուստի ազատ թրթռումները աստիճանաբար մարում են (նկ. 6):

Հարկադիր թրթռումներ- սրանք տատանումներ են, որոնք կատարվում են համակարգի կողմից արտաքին ուժի ազդեցության տակ, որը ժամանակի ընթացքում պարբերաբար փոփոխվում է (այսպես կոչված, շարժիչ ուժ):

Ենթադրենք, որ համակարգի տատանումների բնական հաճախականությունը հավասար է , իսկ շարժիչ ուժը կախված է ժամանակից՝ ներդաշնակ օրենքի համաձայն.

Որոշ ժամանակի ընթացքում հաստատվում են հարկադիր տատանումներ. համակարգը կատարում է բարդ շարժում, որը հարկադիր և ազատ տատանումների սուպերպոզիցիա է։ Ազատ տատանումները աստիճանաբար մարում են, և կայուն վիճակում համակարգը կատարում է հարկադիր տատանումներ, որոնք նույնպես ներդաշնակ են ստացվում։ Հաստատուն հարկադիր տատանումների հաճախականությունը համընկնում է հաճախականության հետ
ստիպող ուժ (արտաքին ուժը, կարծես, իր հաճախականությունը պարտադրում է համակարգին):

Սահմանված հարկադիր տատանումների ամպլիտուդը կախված է շարժիչ ուժի հաճախականությունից։ Այս կախվածության գրաֆիկը ներկայացված է Նկ. 7.

Բրինձ. 7. Ռեզոնանս

Մենք տեսնում ենք, որ ռեզոնանսը տեղի է ունենում հաճախականության մոտ՝ հարկադիր տատանումների ամպլիտուդի մեծացման ֆենոմենը։ Ռեզոնանսային հաճախականությունը մոտավորապես հավասար է համակարգի տատանումների բնական հաճախությանը. Շփման բացակայության դեպքում ռեզոնանսային հաճախականությունը համընկնում է տատանումների բնական հաճախականության հետ, իսկ տատանումների ամպլիտուդը մեծանում է մինչև անսահմանություն:

Մենք ուսումնասիրեցինք մի քանի ֆիզիկապես բոլորովին տարբեր համակարգեր և համոզվեցինք, որ շարժման հավասարումները վերածվում են նույն ձևի

Ֆիզիկական համակարգերի միջև տարբերությունները հայտնվում են միայն տարբեր սահմանումքանակները և տարբեր ֆիզիկական զգացողությունփոփոխական x: սա կարող է լինել կոորդինատ, անկյուն, լիցք, հոսանք և այլն: Նկատի ունեցեք, որ այս դեպքում, ինչպես հետևում է հենց հավասարման կառուցվածքից (1.18), մեծությունը միշտ ունի հակադարձ ժամանակի չափ:

Հավասարումը (1.18) նկարագրում է այսպես կոչված ներդաշնակ թրթռումներ.

Հարմոնիկ թրթռման հավասարումը (1.18) երկրորդ կարգի գծային դիֆերենցիալ հավասարում է (քանի որ այն պարունակում է փոփոխականի երկրորդ ածանցյալը. x). Հավասարման գծայինությունը նշանակում է, որ

եթե ինչ-որ գործառույթ x(t)այս հավասարման լուծումն է, ապա ֆունկցիան Cx(t)կլինի նաև նրա լուծումը ( Գ- կամայական հաստատուն);

եթե գործառույթներ x 1 (տ)Եվ x 2 (տ)այս հավասարման լուծումներն են, ապա դրանց գումարը x 1 (տ) + x 2 (տ)կլինի նաև նույն հավասարման լուծումը:

Ապացուցված է նաև մաթեմատիկական թեորեմ, ըստ որի երկրորդ կարգի հավասարումն ունի երկու անկախ լուծում։ Մնացած բոլոր լուծումները, ըստ գծայինության հատկությունների, կարելի է ստանալ որպես դրանց գծային համակցություններ։ Ուղղակի տարբերակմամբ հեշտ է ստուգել, ​​որ անկախությունը գործում է և բավարարում է հավասարումը (1.18): Սա նշանակում է, որ այս հավասարման ընդհանուր լուծումն ունի ձև.

Որտեղ C 1,C 2- կամայական հաստատուններ. Այս լուծումը կարող է ներկայացվել մեկ այլ ձևով. Եկեք մուտքագրենք արժեքը

և անկյունը որոշիր հարաբերություններով.

Այնուհետև ընդհանուր լուծումը (1.19) գրվում է այսպես

Ըստ եռանկյունաչափության բանաձևերի՝ փակագծերում արտահայտությունը հավասար է

Վերջապես գալիս ենք ներդաշնակ թրթռման հավասարման ընդհանուր լուծումորպես:

Ոչ բացասական արժեք Ականչեց թրթռման ամպլիտուդ, - տատանումների սկզբնական փուլը. Կոսինուսի ամբողջ արգումենտը՝ համակցությունը, կոչվում է տատանումների փուլ.

(1.19) և (1.23) արտահայտությունները լիովին համարժեք են, ուստի մենք կարող ենք օգտագործել դրանցից որևէ մեկը՝ ելնելով պարզության նկատառումներից: Երկու լուծումներն էլ ժամանակի պարբերական ֆունկցիաներ են։ Իրոք, սինուսը և կոսինուսը պարբերական են կետով . Հետևաբար, ներդաշնակ տատանումներ կատարող համակարգի տարբեր վիճակներ կրկնվում են որոշ ժամանակ անց տ*, որի ընթացքում տատանման փուլը ստանում է աճ, որը բազմապատիկ է :

Դրանից բխում է, որ

Այս ժամանակներից ամենաքիչը

կանչեց տատանումների ժամանակաշրջան (նկ. 1.8), իսկ - իր շրջանաձև (ցիկլային) հաճախականությունը.

Բրինձ. 1.8.

Նրանք նաև օգտագործում են հաճախականությունը տատանումներ

Համապատասխանաբար, շրջանաձև հաճախականությունը հավասար է մեկ տատանումների քանակին վայրկյան

Այսպիսով, եթե համակարգը ժամանակին տբնութագրվում է փոփոխականի արժեքով x (t),ապա որոշ ժամանակ անց փոփոխականը կունենա նույն արժեքը (նկ. 1.9), այսինքն

Նույն իմաստը բնականաբար ժամանակի ընթացքում կկրկնվի 2Տ, ԶՏև այլն:

Բրինձ. 1.9. Տատանումների ժամանակաշրջան

Ընդհանուր լուծումը ներառում է երկու կամայական հաստատուններ ( C 1, C 2կամ Ա, ա), որոնց արժեքները պետք է որոշվեն երկուով նախնական պայմանները. Սովորաբար (թեև ոչ պարտադիր) նրանց դերը խաղում է փոփոխականի սկզբնական արժեքներով x(0)և դրա ածանցյալը։

Օրինակ բերենք. Հարմոնիկ տատանումների հավասարման լուծումը (1.19) թող նկարագրի զսպանակային ճոճանակի շարժումը։ Կամայական հաստատունների արժեքները կախված են նրանից, թե ինչպես ենք մենք ճոճանակը հանել հավասարակշռությունից: Օրինակ, մենք գարունը քաշեցինք հեռավորության վրա և բաց թողեց գնդակը առանց նախնական արագության: Այս դեպքում

Փոխարինող t = 0(1.19), մենք գտնում ենք հաստատունի արժեքը C 2

Այսպիսով, լուծումն ունի հետևյալ տեսքը.

Բեռի արագությունը մենք գտնում ենք ժամանակի նկատմամբ տարբերակմամբ

Փոխարինելով այստեղ տ = 0, գտե՛ք հաստատունը Գ 1:

Վերջապես

Համեմատելով (1.23) հետ՝ գտնում ենք, որ տատանումների ամպլիտուդն է, և դրա սկզբնական փուլը զրո է.

Հիմա եկեք այլ կերպ անհավասարակշռենք ճոճանակը: Բեռին այնպես խփենք, որ այն նախնական արագություն ձեռք բերի, բայց հարվածի ժամանակ գործնականում չշարժվի։ Այնուհետև մենք ունենք այլ նախնական պայմաններ.

մեր լուծումը կարծես

Բեռի արագությունը կփոխվի օրենքի համաձայն.

Այստեղ փոխարինենք.

Այս բաժինն ուսումնասիրելիս խնդրում ենք նկատի ունենալ, որ տատանումներտարբեր ֆիզիկական բնույթի նկարագրված են ընդհանուր մաթեմատիկական դիրքերից: Այստեղ անհրաժեշտ է հստակ հասկանալ այնպիսի հասկացություններ, ինչպիսիք են ներդաշնակ տատանումը, փուլը, փուլային տարբերությունը, ամպլիտուդը, հաճախականությունը, տատանումների ժամանակաշրջանը։

Պետք է նկատի ունենալ, որ ցանկացած իրական տատանողական համակարգում կա միջավայրի դիմադրություն, այսինքն. տատանումները կխոնավվեն։ Տատանումների մարումը բնութագրելու համար ներկայացվում են մարման գործակից և լոգարիթմական մարման նվազում:

Եթե ​​տատանումները տեղի են ունենում արտաքին, պարբերաբար փոփոխվող ուժի ազդեցությամբ, ապա այդպիսի տատանումները կոչվում են հարկադիր։ Դրանք չխոնավեցվելու են: Հարկադիր տատանումների ամպլիտուդը կախված է շարժիչ ուժի հաճախականությունից։ Երբ հարկադիր տատանումների հաճախականությունը մոտենում է բնական տատանումների հաճախականությանը, հարկադրված տատանումների ամպլիտուդը կտրուկ մեծանում է։ Այս երեւույթը կոչվում է ռեզոնանս։

Էլեկտրամագնիսական ալիքների ուսումնասիրությանն անցնելիս պետք է դա հստակ հասկանալէլեկտրամագնիսական ալիքտիեզերքում տարածվող էլեկտրամագնիսական դաշտ է։ Էլեկտրամագնիսական ալիքներ արձակող ամենապարզ համակարգը էլեկտրական դիպոլն է։ Եթե ​​դիպոլը ենթարկվում է ներդաշնակ տատանումների, ապա այն արձակում է միագույն ալիք։

Բանաձևերի աղյուսակ. տատանումներ և ալիքներ

Արտաքին, պարբերաբար փոփոխվող ուժերի ազդեցության տակ առաջացող տատանումներ (արտաքինից դեպի տատանողական համակարգ էներգիայի պարբերական մատակարարմամբ)

Էներգիայի փոխակերպում

Գարնանային ճոճանակ

Տատանումների ցիկլային հաճախականությունը և ժամանակաշրջանը համապատասխանաբար հավասար են.

Նյութական կետամրացված է կատարյալ առաձգական աղբյուրի վրա

Ø Զսպանակային ճոճանակի ներուժի և կինետիկ էներգիայի կախվածության գրաֆիկը x կոորդինատից:

Ø ժամանակի համեմատ կինետիկ և պոտենցիալ էներգիայի որակական գրաֆիկներ:

Ø Ստիպված

Ø Հարկադիր տատանումների հաճախականությունը հավասար է արտաքին ուժի փոփոխության հաճախականությանը

Ø Եթե ​​Fbc-ն փոխվում է սինուսի կամ կոսինուսի օրենքի համաձայն, ապա հարկադիր տատանումները ներդաշնակ կլինեն

Ø Ինքնատատանումներով անհրաժեշտ է պարբերաբար էներգիա մատակարարել սեփական աղբյուրից տատանողական համակարգի ներսում։

Հարմոնիկ տատանումները տատանումներ են, որոնց ժամանակ տատանվող մեծությունը փոխվում է սինուսի կամ կոսինուսի օրենքի համաձայն։

Հարմոնիկ տատանումների հավասարումները (կետերի շարժման օրենքները) ունեն ձև

Հարմոնիկ թրթռումներ կոչվում են այնպիսի տատանումներ, որոնցում տատանվող մեծությունը ժամանակի հետ փոփոխվում է օրենքի համաձայնսինուս կամկոսինուս .
Հարմոնիկ հավասարում ունի ձև.

,
որտեղ Ա - թրթռման ամպլիտուդ (համակարգի ամենամեծ շեղման մեծությունը հավասարակշռության դիրքից); -շրջանաձև (ցիկլային) հաճախականություն: Կոսինուսի պարբերաբար փոփոխվող փաստարկը կոչվում է տատանումների փուլ . Տատանման փուլը որոշում է տատանվող մեծության տեղաշարժը հավասարակշռության դիրքից տվյալ պահին t. Ֆ հաստատունը ներկայացնում է փուլային արժեքը t = 0 պահին և կոչվում է տատանումների սկզբնական փուլը . Սկզբնական փուլի արժեքը որոշվում է հղման կետի ընտրությամբ: X արժեքը կարող է ընդունել արժեքներ՝ սկսած -A-ից մինչև +A:
T ժամանակային միջակայքը, որի միջոցով կրկնվում են տատանողական համակարգի որոշակի վիճակներ, կոչվում է տատանումների ժամանակաշրջան . Կոսինուսը 2π պարբերությամբ պարբերական ֆունկցիա է, հետևաբար, T ժամանակահատվածում, որից հետո տատանման փուլը կստանա 2π-ի հավասար աճ, ներդաշնակ տատանումներ կատարող համակարգի վիճակը կկրկնվի։ T ժամանակի այս հատվածը կոչվում է ներդաշնակ տատանումների ժամանակաշրջան։
Հարմոնիկ տատանումների ժամանակաշրջանը հավասար է T = 2π/.
Տատանումների թիվը միավոր ժամանակում կոչվում է թրթռումների հաճախականությունը ν.
Հարմոնիկ հաճախականություն հավասար է՝ ν = 1/Տ։ Հաճախականության միավոր հերց(Հց) - մեկ տատանում մեկ վայրկյանում:
Շրջանաձև հաճախականությունը = 2π/T = 2πν տալիս է տատանումների քանակը 2π վայրկյանում։

Ընդհանրացված ներդաշնակ տատանում դիֆերենցիալ ձևով

Գրաֆիկորեն ներդաշնակ տատանումները կարելի է պատկերել որպես x-ի կախվածություն t-ից (նկ. 1.1.Ա), և պտտվող ամպլիտուդի մեթոդ (վեկտորային դիագրամի մեթոդ)(նկ.1.1.Բ) .

Պտտվող ամպլիտուդի մեթոդը թույլ է տալիս պատկերացնել ներդաշնակ թրթռման հավասարման մեջ ներառված բոլոր պարամետրերը: Իսկապես, եթե ամպլիտուդի վեկտորը Ագտնվում է x-ի առանցքի φ անկյան տակ (տես նկար 1.1. B), ապա դրա պրոյեկցիան x առանցքի վրա հավասար կլինի՝ x = Acos(φ): φ անկյունը սկզբնական փուլն է: Եթե ​​վեկտորը Ապտտման մեջ բերել հետ անկյունային արագություն, հավասար է տատանումների շրջանաձև հաճախականությանը, այնուհետև վեկտորի վերջի պրոյեկցիան կշարժվի x առանցքի երկայնքով և կընդունի -A-ից +A արժեքներ, և այս պրոեկցիայի կոորդինատը ժամանակի ընթացքում կփոխվի՝ համաձայն օրենք:
.
Այսպիսով, վեկտորի երկարությունը հավասար է ներդաշնակ տատանման ամպլիտուդիային, վեկտորի ուղղությունը սկզբնական պահին կազմում է անկյուն x առանցքով, որը հավասար է φ տատանումների սկզբնական փուլին, իսկ ուղղության անկյան փոփոխությունը. ժամանակի հետ հավասար է ներդաշնակ տատանումների փուլին: Ժամանակը, որի ընթացքում ամպլիտուդային վեկտորը կատարում է մեկ ամբողջական պտույտ, հավասար է ներդաշնակ տատանումների T պարբերությանը։ Վեկտորային պտույտների թիվը վայրկյանում հավասար է տատանումների հաճախականությանը ν։

Մաքսվելի տեսության հիմունքները էլեկտրամագնիսական դաշտի համար

Vortex էլեկտրական դաշտ

Ֆարադեի օրենքից ξ=dՖ/dtհետևում է դրան ցանկացածՇղթայի հետ կապված մագնիսական ինդուկցիայի հոսքի փոփոխությունը հանգեցնում է ինդուկցիայի էլեկտրաշարժիչ ուժի առաջացմանը և, որպես հետևանք, առաջանում է ինդուկցիոն հոսանք: Հետեւաբար, էմֆ. Էլեկտրամագնիսական ինդուկցիան հնարավոր է նաև փոփոխական մագնիսական դաշտում տեղակայված անշարժ շղթայում։ Այնուամենայնիվ, e.m.f. ցանկացած շղթայում տեղի է ունենում միայն այն ժամանակ, երբ արտաքին ուժերը գործում են դրա մեջ գտնվող ընթացիկ կրիչների վրա՝ ոչ էլեկտրաստատիկ ծագման ուժեր (տես § 97): Ուստի հարց է առաջանում տվյալ դեպքում արտաքին ուժերի բնույթի մասին։

Փորձը ցույց է տալիս, որ այս կողմնակի ուժերը կապված չեն շղթայում ընթացող ոչ ջերմային, ոչ էլ քիմիական գործընթացների հետ. դրանց առաջացումը նույնպես չի կարող բացատրվել Լորենցի ուժերով, քանի որ նրանք չեն գործում անշարժ լիցքերով: Մաքսվելը ենթադրեց, որ ցանկացած փոփոխական մագնիսական դաշտ գրգռում է շրջակա տարածության էլեկտրական դաշտը, որը

և հանդիսանում է շղթայում ինդուկտիվ հոսանքի առաջացման պատճառը: Մաքսվելի պատկերացումների համաձայն, շղթան, որում հայտնվում է emf-ը, երկրորդական դեր է խաղում՝ լինելով մի տեսակ միայն «սարք», որը հայտնաբերում է այս դաշտը:

առաջին հավասարումըՄաքսվելը նշում է, որ էլեկտրական դաշտի փոփոխությունները առաջացնում են պտտվող մագնիսական դաշտ։

Երկրորդ հավասարումըՄաքսվելն արտահայտում է Ֆարադեյի էլեկտրամագնիսական ինդուկցիայի օրենքը. Էմֆ-ը ցանկացած փակ օղակում հավասար է մագնիսական հոսքի փոփոխության արագությանը (այսինքն՝ ժամանակի ածանցյալին): Բայց EMF-ը հավասար է էլեկտրական դաշտի ուժգնության վեկտորի E շոշափող բաղադրիչին, որը բազմապատկվում է շղթայի երկարությամբ: Ռոտորին անցնելու համար, ինչպես Մաքսվելի առաջին հավասարման մեջ, բավական է emf-ը բաժանել եզրագծի մակերեսի վրա և վերջինս ուղղել զրոյի, այսինքն՝ վերցնել մի փոքր ուրվագիծ, որը ծածկում է դիտարկվող տարածության կետը (նկ. 9, գ). Այնուհետև հավասարման աջ կողմում այլևս չի լինի հոսք, այլ մագնիսական ինդուկցիա, քանի որ հոսքը հավասար է ինդուկցիային, որը բազմապատկվում է շղթայի տարածքով:
Այսպիսով, մենք ստանում ենք. rotE = - dB/dt:
Այսպիսով, պտտվող էլեկտրական դաշտը առաջանում է մագնիսական դաշտի փոփոխությունների արդյունքում, որը ցույց է տրված Նկ. 9,c և ներկայացված է հենց նոր տրված բանաձևով:
Երրորդ և չորրորդ հավասարումներ Maxwell-ը զբաղվում է մեղադրանքներով և դրանց կողմից առաջացած դաշտերով: Դրանք հիմնված են Գաուսի թեորեմի վրա, որն ասում է, որ էլեկտրական ինդուկցիայի վեկտորի հոսքը ցանկացած փակ մակերևույթի միջով հավասար է այդ մակերեսի ներսում գտնվող լիցքին։

Մի ամբողջ գիտություն հիմնված է Մաքսվելի հավասարումների վրա՝ էլեկտրադինամիկա, որը թույլ է տալիս լուծել շատ օգտակար խնդիրներ՝ օգտագործելով խիստ մաթեմատիկական մեթոդներ: գործնական խնդիրներ. Հնարավոր է հաշվարկել, օրինակ, տարբեր ալեհավաքների ճառագայթման դաշտը ինչպես ազատ տարածության մեջ, այնպես էլ Երկրի մակերեսին մոտ կամ ինքնաթիռի մարմնի մոտ, օրինակ՝ ինքնաթիռի կամ հրթիռի։ Էլեկտրոդինամիկան հնարավորություն է տալիս հաշվարկել ալիքատարների և խոռոչի ռեզոնատորների դիզայնը՝ սարքեր, որոնք օգտագործվում են շատ բարձր հաճախականություններով սանտիմետր և միլիմետր ալիքների միջակայքում, որտեղ սովորական հաղորդման գծերը և տատանողական սխեմաները այլևս հարմար չեն: Առանց էլեկտրադինամիկայի, ռադարների, տիեզերական ռադիոհաղորդումների, ալեհավաքի տեխնոլոգիայի և ժամանակակից ռադիոտեխնիկայի շատ այլ ոլորտների զարգացումն անհնար կլիներ:

Կողմնակալ հոսանք

ՏԵՂԱՓՈԽԱԿԱՆ ԸՆԹԱՑՔ, արժեք, որը համաչափ է դիէլեկտրիկում կամ վակուումում փոփոխական էլեկտրական դաշտի փոփոխության արագությանը։ «Հոսանք» անվանումը պայմանավորված է նրանով, որ տեղաշարժի հոսանքը, ինչպես հաղորդման հոսանքը, առաջացնում է մագնիսական դաշտ:

Էլեկտրամագնիսական դաշտի տեսությունը կառուցելիս Ջ. Ք. Մաքսվելն առաջ քաշեց մի վարկած (հետագայում փորձնականորեն հաստատվեց), որ մագնիսական դաշտը ստեղծվում է ոչ միայն լիցքերի (հաղորդման հոսանքի, կամ պարզապես հոսանքի) շարժմամբ, այլև ժամանակի ցանկացած փոփոխությամբ։ էլեկտրական դաշտը։

Տեղաշարժման հոսանքի հայեցակարգը ներկայացվել է Մաքսվելի կողմից՝ փոփոխության միջև քանակական հարաբերություններ հաստատելու համար էլեկտրական դաշտև դրա առաջացրած մագնիսական դաշտը:

Համաձայն Մաքսվելի տեսության՝ կոնդենսատոր պարունակող փոփոխական հոսանքի միացումում կոնդենսատորի փոփոխական էլեկտրական դաշտը ժամանակի յուրաքանչյուր ակնթարթում ստեղծում է նույն մագնիսական դաշտը, որը կստեղծվեր հոսանքով (կոչվում է տեղաշարժի հոսանք), եթե այն հոսեր թիթեղների միջև։ կոնդենսատորը. Այս սահմանումից բխում է, որ J սմ = J(այսինքն, հաղորդման հոսանքի խտության և տեղահանման հոսանքի խտության թվային արժեքները հավասար են), և, հետևաբար, հաղորդիչի ներսում հաղորդիչ հոսանքի խտության գծերը շարունակաբար վերածվում են կոնդենսատորի թիթեղների միջև տեղաշարժման հոսանքի խտության գծերի: Շեղումների հոսանքի խտությունը ժ սմբնութագրում է էլեկտրական ինդուկցիայի փոփոխության արագությունը Դժամանակին:

J սմ = + ?D/?t.

Տեղաշարժման հոսանքը չի արտադրում Ջուլի ջերմություն ֆիզիկական սեփականություն- շրջակա տարածքում մագնիսական դաշտ ստեղծելու ունակություն.

Շրջանաձև մագնիսական դաշտը ստեղծվում է ընդհանուր հոսանքի միջոցով, որի խտությունը կազմում է ժ, հավասար է հաղորդման հոսանքի խտության և տեղաշարժման հոսանքի գումարին.D/?t. Այդ իսկ պատճառով ներմուծվել է հոսանքի անվանումը ?D/?t քանակի համար։

Հարմոնիկ օսլիլատորտատանվող համակարգ է, որը նկարագրված է d 2 s/dt 2 + ω 0 2 s = 0 կամ արտահայտությամբ։

որտեղ վերը նշված երկու կետերը նշանակում են ժամանակի կրկնակի տարբերակում: Կարևոր օրինակ են հարմոնիկ տատանումների տատանումները պարբերական շարժումև ծառայել որպես ճշգրիտ կամ մոտավոր մոդել դասական և քվանտային ֆիզիկայի բազմաթիվ խնդիրներում։ Ներդաշնակ տատանումների օրինակներ են զսպանակային ճոճանակները, ֆիզիկական և մաթեմատիկական ճոճանակները և տատանողական սխեման (հոսանքների և լարումների համար այնքան փոքր, որ շղթայի տարրերը կարելի է համարել գծային):

Հարմոնիկ թրթռումներ

Մեխանիկայի մեջ մարմինների թարգմանական և պտտվող շարժումների հետ մեկտեղ էական հետաքրքրություն են ներկայացնում նաև տատանողական շարժումները։ Մեխանիկական թրթռումները կոչվում են մարմինների շարժումներ, որոնք կրկնվում են ճշգրիտ (կամ մոտավորապես) ժամանակի հավասար ընդմիջումներով: Տատանվող մարմնի շարժման օրենքը սահմանվում է ժամանակի որոշակի պարբերական ֆունկցիայի միջոցով x = զ (տ). Գրաֆիկական պատկերԱյս ֆունկցիան տալիս է ժամանակի ընթացքում տատանողական գործընթացի ընթացքի տեսողական ներկայացում:

Պարզ տատանողական համակարգերի օրինակներ են բեռնվածությունը զսպանակի կամ մաթեմատիկական ճոճանակի վրա (նկ. 2.1.1):

Մեխանիկական թրթռումները, ինչպես ցանկացած այլ ֆիզիկական բնույթի տատանողական պրոցեսներ, կարող են լինել անվճարԵվ հարկադրված. Անվճար թրթռումներ կատարվում են ազդեցության տակ ներքին ուժերհամակարգը հավասարակշռությունից դուրս բերելուց հետո: Զսպանակի վրա ծանրության տատանումները կամ ճոճանակի տատանումները ազատ տատանումներ են։ Ազդեցության տակ առաջացող թրթռումներ արտաքինպարբերաբար փոփոխվող ուժերը կոչվում են հարկադրված Տատանողական գործընթացի ամենապարզ տեսակը պարզ է ներդաշնակ թրթռումներ , որոնք նկարագրված են հավասարմամբ

Տատանումների հաճախականությունը զցույց է տալիս, թե քանի տատանում է տեղի ունենում 1 վրկ-ում: Հաճախականության միավոր - հերց(Հց): Տատանումների հաճախականությունը զկապված ω ցիկլային հաճախականության և տատանումների ժամանակաշրջանի հետ Տհարաբերակցությունները:

տալիս է տատանվող մեծության կախվածությունը Սժամանակից տ; սա բացահայտ ձևով ազատ ներդաշնակ տատանումների հավասարումն է: Այնուամենայնիվ, սովորաբար թրթռման հավասարումը ընկալվում է որպես այս հավասարման այլ ներկայացում, դիֆերենցիալ ձևով: Որոշակիության համար վերցնենք (1) հավասարումը ձևով

Եկեք այն երկու անգամ տարբերենք ժամանակի առումով.

Կարելի է տեսնել, որ հետևյալ հարաբերություններն են.

որը կոչվում է ազատ ներդաշնակ տատանումների հավասարում (դիֆերենցիալ տեսքով)։ Հավասարումը (1) դիֆերենցիալ (2) հավասարման լուծումն է: Քանի որ հավասարումը (2) է դիֆերենցիալ հավասարումԵրկրորդ կարգի, ամբողջական լուծում ստանալու համար անհրաժեշտ է երկու նախնական պայման (այսինքն՝ որոշել (1) հավասարման մեջ ներառված հաստատունները. Աև j 0); օրինակ՝ տատանողական համակարգի դիրքն ու արագությունը ժամը տ = 0.

Նույն ուղղության և նույն հաճախականության ներդաշնակ թրթիռների ավելացում: Beats

Թող լինեն նույն ուղղության և նույն հաճախականության երկու ներդաշնակ տատանումներ

Ստացված տատանման հավասարումը կունենա ձև

Եկեք ստուգենք դա՝ ավելացնելով համակարգի հավասարումները (4.1)

Կիրառելով կոսինուսների գումարի թեորեմը և կատարել հանրահաշվական փոխակերպումներ.

Հնարավոր է գտնել A-ի և φ0-ի այնպիսի արժեքներ, որ հավասարումները բավարարվեն

Համարելով (4.3) երկու հավասարումներ A և φ0 անհայտներով, մենք գտնում ենք՝ քառակուսի դնելով և գումարելով դրանք, իսկ հետո երկրորդը բաժանելով առաջինի վրա.

(4.3) փոխարինելով (4.2)՝ մենք ստանում ենք.

Կամ վերջապես, օգտագործելով կոսինուսների գումարի թեորեմը, մենք ունենք.

Մարմինը, մասնակցելով նույն ուղղության և նույն հաճախականության երկու ներդաշնակ տատանումների, կատարում է նաև ներդաշնակ տատանումներ նույն ուղղությամբ և նույն հաճախականությամբ, ինչ ավելացված տատանումները։ Ստացված տատանումների ամպլիտուդը կախված է հարթեցված տատանումների փուլային տարբերությունից (φ2-φ1):

Կախված փուլային տարբերությունից (φ2-φ1):

1) (φ2-φ1) = ±2մπ (m=0, 1, 2, …), ապա A= A1+A2, այսինքն՝ ստացված A տատանման ամպլիտուդը հավասար է ավելացված տատանումների ամպլիտուդների գումարին.

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, ...), ապա A= |A1-A2|, այսինքն՝ ստացված տատանման ամպլիտուդը հավասար է տարբերությանը. ավելացված տատանումների ամպլիտուդներում

Թրթռումների ամպլիտուդի պարբերական փոփոխությունները, որոնք տեղի են ունենում, երբ միանման հաճախականություններով երկու ներդաշնակ թրթռումներ գումարվում են, կոչվում են հարվածներ:

Թող երկու տատանումները հաճախականությամբ քիչ տարբերվեն: Այնուհետև ավելացված տատանումների ամպլիտուդները հավասար են A-ի, իսկ հաճախականությունները հավասար են ω-ի և ω+Δω-ի, իսկ Δω շատ փոքր է ω-ից։ Մենք ընտրում ենք մեկնարկային կետը, որպեսզի երկու տատանումների սկզբնական փուլերը հավասար լինեն զրոյի.

Եկեք լուծենք համակարգը

Համակարգային լուծում.

Ստացված տատանումը կարելի է համարել ներդաշնակ ω հաճախականությամբ, A ամպլիտուդով, որը տատանվում է հետևյալ կերպ. պարբերական օրենք:

Ա-ի փոփոխության հաճախականությունը կրկնակի է կոսինուսի փոփոխության հաճախականությունից։ Զարկերի հաճախականությունը հավասար է ավելացված տատանումների հաճախականությունների տարբերությանը. ωb = Δω

Հարվածային շրջան.

Հնչյունի հաճախականության որոշումը (հղման որոշակի բարձրության ձայնը հղումով և չափված թրթռումներով չափված արժեքը հղման արժեքի հետ համեմատելու ամենատարածված մեթոդն է: Բիթ մեթոդը օգտագործվում է երաժշտական ​​գործիքների լարման, լսողության վերլուծության և այլնի համար: .

Առնչվող տեղեկություններ.