Triqonometrik funksiyaların hədlərinin tapılması nümunələri. İlk diqqətəlayiq hədd: tapma nümunələri, problemlər və ətraflı həllər. Tərs triqonometrik funksiyalar
Yuxarıdakı məqalədən limitin nə olduğunu və nə ilə yeyildiyini öyrənə bilərsiniz - bu ÇOX vacibdir. Niyə? Determinantların nə olduğunu başa düşməyə və onları uğurla həll etməyə, törəmənin nə olduğunu heç başa düşməyə və onları “beşlik”də tapa bilməzsiniz. Ancaq limitin nə olduğunu başa düşmürsənsə, praktiki vəzifələri həll etmək çətin olacaq. Həmçinin, qərarların dizayn nümunələri və dizayn üçün tövsiyələrimlə tanış olmaq artıq olmaz. Bütün məlumatlar sadə və əlçatan bir şəkildə təqdim olunur.
Və bu dərsin məqsədləri üçün bizə aşağıdakı metodik materiallar lazımdır: Möhtəşəm Limitlər Və Triqonometrik düsturlar. Onları səhifədə tapa bilərsiniz. Təlimatları çap etmək daha yaxşıdır - bu, daha rahatdır, bundan əlavə, onlara tez-tez oflayn daxil olmaq lazımdır.
Möhtəşəm məhdudiyyətlər haqqında nə diqqətəlayiqdir? Bu hədlərin əlamətdarlığı ondan ibarətdir ki, onlar məşhur riyaziyyatçıların ən böyük ağılları tərəfindən sübut edilmişdir və minnətdar nəsillər triqonometrik funksiyalar, loqarifmlər və dərəcələr yığını ilə qorxunc məhdudiyyətlərdən əziyyət çəkməli deyillər. Yəni limitləri taparkən nəzəri cəhətdən sübut olunmuş hazır nəticələrdən istifadə edəcəyik.
Bir neçə əlamətdar məhdudiyyət var, lakin praktikada qiyabi təhsil alan tələbələrin 95% hallarda iki əlamətdar həddi var: İlk gözəl hədd, İkinci gözəl hədd. Qeyd etmək lazımdır ki, bunlar tarixən müəyyən edilmiş adlardır və məsələn, "ilk gözəl həddi" haqqında danışarkən, bununla tavandan götürülmüş təsadüfi bir hədd deyil, çox konkret bir şeyi nəzərdə tuturlar.
İlk gözəl hədd
Aşağıdakı həddi nəzərdən keçirin: (doğma "o" hərfinin əvəzinə mən yunan "alfa" hərfindən istifadə edəcəyəm, bu, materialın təqdimatı baxımından daha əlverişlidir).
Məhdudiyyətlərin tapılması qaydamıza uyğun olaraq (məqaləyə bax Limitlər. Həll nümunələri) funksiyada sıfırı əvəz etməyə çalışırıq: paylayıcıda sıfır alırıq (sıfırın sinusu sıfırdır), məxrəcdə, açıq-aydın, sıfır da. Beləliklə, xoşbəxtlikdən açıqlanmağa ehtiyacı olmayan forma qeyri-müəyyənliyi ilə qarşılaşırıq. Riyazi analiz zamanı sübut olunur ki:
Bu riyazi fakt deyilir İlk gözəl hədd. Həddinin analitik sübutunu verməyəcəyəm, lakin onun həndəsi mənasını dərsdə nəzərdən keçirəcəyik sonsuz kiçik funksiyalar.
Çox vaxt praktiki tapşırıqlarda funksiyalar fərqli şəkildə təşkil edilə bilər, bu heç nəyi dəyişmir:
– eyni ilk gözəl hədd.
Ancaq siz say və məxrəci özünüz dəyişdirə bilməzsiniz! Şəklində limit verilirsə, o zaman heç nəyi yenidən təşkil etmədən eyni formada həll edilməlidir.
Praktikada təkcə dəyişən parametr deyil, həm də elementar funksiya, kompleks funksiya kimi çıxış edə bilər. Yalnız sıfıra meyl etməsi vacibdir.
Nümunələr:
, , ![]() ,
, ![]()
Budur, , , ![]() , və hər şey uğuldayır - ilk gözəl limit tətbiq olunur.
, və hər şey uğuldayır - ilk gözəl limit tətbiq olunur.
Və burada növbəti giriş - bidət:

Niyə? Çoxhədli sıfıra meyl etmədiyi üçün beşə meyllidir.
Yeri gəlmişkən, sual doldurulma ilə bağlıdır, amma hədd nədir ![]() ? Cavabı dərsin sonunda tapmaq olar.
? Cavabı dərsin sonunda tapmaq olar.
Praktikada hər şey o qədər də hamar deyil, demək olar ki, heç vaxt tələbəyə pulsuz limiti həll etmək və asan kredit almaq təklif edilməyəcək. Hmmm... Mən bu sətirləri yazıram və ağlıma çox vacib bir fikir gəldi - axı, “sərbəst” riyazi tərifləri və düsturları əzbər xatırlamaq daha yaxşı görünür, bu, test zamanı əvəzsiz kömək ola bilər. məsələ “iki” və “üç” arasında həll olunacaq və müəllim şagirdə sadə sual vermək və ya ən sadə misalı həll etməyi təklif etmək qərarına gəlir (“bəlkə o (a) hələ nə bilir?!”).
Praktik nümunələrə keçək:
Misal 1
Həddini tapın
Əgər limitdə bir sinus görsək, bu, bizi dərhal ilk diqqətəlayiq həddi tətbiq etməyin mümkünlüyü barədə düşünməyə vadar etməlidir.
Əvvəlcə limit işarəsi altındakı ifadədə 0-ı əvəz etməyə çalışırıq (bunu zehni olaraq və ya qaralamada edirik):
Deməli, bizdə formanın qeyri-müəyyənliyi var, onun göstərməyə əmin olun qərar qəbul edərkən. Limit işarəsi altındakı ifadə ilk gözəl həddi xatırladır, lakin bu, tam deyil, sinusun altındadır, lakin məxrəcdədir.
Belə hallarda, süni bir cihazdan istifadə edərək, ilk diqqətəlayiq həddi özümüz təşkil etməliyik. Əsaslandırma xətti belə ola bilər: “bizdə olan sinusun altında, bu o deməkdir ki, biz də məxrəcə girməliyik”.
Və bu çox sadə şəkildə edilir:

Yəni məxrəc bu halda süni şəkildə 7-yə vurulur və eyni yeddiyə bölünür. İndi rekord tanış formanı alıb.
Tapşırıq əl ilə tərtib edildikdə, ilk gözəl həddi sadə bir qələmlə qeyd etmək məsləhətdir:

Nə olub? Əslində, dairəvi ifadə vahidə çevrildi və məhsulda yox oldu: 
İndi yalnız üç mərtəbəli fraksiyadan xilas olmaq qalır: 
Çoxmərtəbəli fraksiyaların sadələşdirilməsini kim unutdusa, lütfən, istinad kitabındakı materialı yeniləyin İsti məktəb riyaziyyat düsturları .
Hazır. Yekun cavab:
Əgər qələm işarələrindən istifadə etmək istəmirsinizsə, onda həlli belə formatlaşdırmaq olar:
“![]()
Biz ilk diqqətəlayiq limitdən istifadə edirik 
“
Misal 2
Həddini tapın
Yenə limitdə bir kəsr və sinus görürük. Numerator və məxrəcdə sıfırı əvəz etməyə çalışırıq:
Həqiqətən, qeyri-müəyyənliyimiz var və buna görə də ilk diqqətəlayiq həddi təşkil etməyə çalışmalıyıq. Dərsdə Limitlər. Həll nümunələri biz qaydanı nəzərə aldıq ki, qeyri-müəyyənlik olduqda, biz payı və məxrəci amillərə ayırmalıyıq. Burada - eyni şey, dərəcələri məhsul (çoxalanlar) kimi təqdim edəcəyik:


Əvvəlki misalda olduğu kimi, gözəl sərhədləri qələmlə təsvir edirik (burada onlardan ikisi var) və onların birinə meylli olduğunu göstəririk:

Əslində cavab hazırdır:

Aşağıdakı nümunələrdə mən Paint-də sənətkarlıq etməyəcəyəm, bir dəftərdə bir həlli necə düzgün tərtib etməyi düşünürəm - artıq başa düşürsən.
Misal 3
Həddini tapın
Limit işarəsi altındakı ifadədə sıfırı əvəz edirik:
Açıqlanması lazım olan qeyri-müəyyənlik əldə edilib. Həddində bir tangens varsa, o, demək olar ki, həmişə məşhur triqonometrik düstura görə sinus və kosinusa çevrilir (yeri gəlmişkən, kotangenslə təxminən eyni şeyi edirlər, metodik materiala baxın. İsti triqonometrik düsturlar Səhifədə Riyazi düsturlar, cədvəllər və istinad materialları).
Bu halda:
![]()
Sıfırın kosinusu birinə bərabərdir və ondan qurtulmaq asandır (birə meylli olduğunu qeyd etməyi unutmayın):
Beləliklə, əgər hədddə kosinus ÇOX olarsa, o zaman kobud desək, məhsulda yox olan vahidə çevrilməlidir.

Burada hər şey heç bir vurma və bölmə olmadan daha sadə oldu. İlk əlamətdar hədd də birliyə çevrilir və məhsulda yox olur:

Nəticədə sonsuzluq əldə edilir, olur.
Misal 4
Həddini tapın
Numerator və məxrəcdə sıfırı əvəz etməyə çalışırıq:
![]()
Əldə edilən qeyri-müəyyənlik (sıfır kosinusu, xatırladığımız kimi, birə bərabərdir)
Triqonometrik düsturdan istifadə edirik. Qeyd etmək! Nədənsə, bu düsturdan istifadə edilən məhdudiyyətlər çox yaygındır.
![]()
Həddindən artıq sabit çarpanları çıxarırıq:
İlk diqqətəlayiq həddi təşkil edək:

Burada birinə çevrilən və məhsulda yox olan yalnız bir gözəl limitimiz var:

Gəlin üç mərtəbədən xilas olaq:

Limit əslində həll olundu, qalan sinusun sıfıra meyl etdiyini göstəririk:

Misal 5
Həddini tapın ![]()
Bu nümunə daha mürəkkəbdir, bunu özünüz anlamağa çalışın:

Bəzi məhdudiyyətlər dəyişəni dəyişdirərək 1-ci əlamətdar həddə endirilə bilər, bu barədə bir az sonra məqalədə oxuya bilərsiniz Məhdud Həll Metodları.
İkinci gözəl hədd
Riyazi analiz nəzəriyyəsində sübut edilmişdir ki:
![]()
Bu fakt deyilir ikinci əlamətdar hədd.
İstinad: ![]() irrasional ədəddir.
irrasional ədəddir.
Yalnız dəyişən parametr deyil, həm də kompleks funksiya kimi çıxış edə bilər. Yalnız sonsuzluğa can atması vacibdir.
Misal 6
Həddini tapın
Limit işarəsi altındakı ifadə gücdə olduqda - bu, ikinci gözəl limiti tətbiq etməyə çalışmalı olduğunuz ilk əlamətdir.
Ancaq əvvəlcə, həmişə olduğu kimi, ifadədə sonsuz böyük bir rəqəmi əvəz etməyə çalışırıq, bunun hansı prinsipə əsasən edildiyi, dərsdə təhlil edildi Limitlər. Həll nümunələri.
Bunu nə vaxt görmək asandır dərəcənin əsası və eksponent - , yəni formada qeyri-müəyyənlik var:
![]()
Bu qeyri-müəyyənlik yalnız ikinci əlamətdar həddin köməyi ilə ortaya çıxır. Ancaq tez-tez olduğu kimi, ikinci möcüzə həddi gümüş nimçədə yatmır və onu süni şəkildə təşkil etmək lazımdır. Aşağıdakı kimi əsaslandıra bilərsiniz: bu nümunədə parametr o deməkdir ki, biz də göstəricidə təşkil etməliyik. Bunun üçün bazanı bir gücə qaldırırıq və ifadənin dəyişməməsi üçün onu bir gücə qaldırırıq:

Tapşırıq əl ilə tərtib edildikdə, qələmlə qeyd edirik:

Demək olar ki, hər şey hazırdır, dəhşətli dərəcə gözəl bir məktuba çevrildi:
Eyni zamanda, limit nişanının özü göstəriciyə köçürülür:
Misal 7
Həddini tapın
Diqqət! Bu cür məhdudiyyət çox yaygındır, lütfən, bu nümunəni çox diqqətlə öyrənin.
Biz limit işarəsi altındakı ifadədə sonsuz böyük ədədi əvəz etməyə çalışırıq:
![]()
Nəticə qeyri-müəyyənlikdir. Lakin ikinci diqqətəlayiq hədd formanın qeyri-müəyyənliyinə aiddir. Nə etməli? Siz dərəcənin əsasını çevirməlisiniz. Biz belə mübahisə edirik: məxrəcdə bizdə var, bu o deməkdir ki, biz də payda təşkil etməliyik.
Сos (sonsuzluq) nəyə bərabərdir? və ən yaxşı cavabı aldım
Krab Bark[guru] tərəfindən cavab
heç nə. Sonsuzluq rəqəm deyil. Arqument sonsuzluğa meyl etdikdə kosinus üçün heç bir məhdudiyyət yoxdur.
-dan cavab Kosta Verde[aktiv]
0-dan 180-ə qədər mövcud deyil
-dan cavab Aleksandr Alenitsın[quru]
Arqumenti olanda kosinusun nəyə meyl etdiyini soruşursunuz
sonsuzluğa meyllidir? Belə bir məhdudiyyət yoxdur, kosinus hər zaman
mənfidən artı 1-ə qədər dəyişir. Və ümumiyyətlə, istənilən dövri
eyni sabitə bərabər olmayan funksiya ola bilməz
sonsuzluqda limit.
-dan cavab Amanjolov Timur[quru]
Bu baş vermir. Bucaq ya var, ya da yoxdur. İpucu: cos 100 grad (işarə = 0 (sıfır)) nə olduğunu soruşun. Nadir hallarda kimsə şəhərlər (ruts) haqqında bilir (zarafat, çoxları məktəbə getdi, amma hamı xatırlamır) ... Əslində, bucaq (dərəcə, min., s.) 0-dan 360-a qədərdir. Sonsuz fırlanma kosinusla ölçülə bilməz ... İstinad üçün qeyd edək ki, kosinus birə bərabər olan və göstərilən bucaqda dayanan dirəyin kölgəsidir, işıq şaquli olaraq aşağı düşür...(məktəb)... İctimai yerə tüpürmək qədər sadədir... . Harada olduğunu bilmək vacibdir...
-dan cavab Ekstrapolator[quru]
Bəli, bu olacaq, o əsarət...
Cos nədir, Sin nədir...
Kosinusun dəyəri vaxtaşırı +1-dən -1-ə və yenidən +1-ə dəyişdiyinə görə, arqument sonsuzluğa meyl etdikdə, funksiya +1-dən -1-ə qədər dəyər aralığına sahib olacaqdır.
İlk diqqətəlayiq hədd aşağıdakı bərabərlik adlanır:
\begin(tənlik)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(tənlik)
$\alpha\to(0)$ üçün bizdə $\sin\alpha\to(0)$ olduğuna görə deyirik ki, ilk diqqətəlayiq hədd $\frac(0)(0)$ formasının qeyri-müəyyənliyini ortaya qoyur. Ümumiyyətlə, (1) düsturunda $\alpha$ dəyişəninin əvəzinə sinus işarəsi altında və məxrəcdə iki şərt yerinə yetirildiyi təqdirdə istənilən ifadə yerləşdirilə bilər:
- Sinus işarəsi altındakı və məxrəcdəki ifadələr eyni vaxtda sıfıra meyllidir, yəni. $\frac(0)(0)$ formasının qeyri-müəyyənliyi var.
- Sinus işarəsinin altındakı və məxrəcdəki ifadələr eynidir.
İlk əlamətdar hədddən gələn nəticələr də tez-tez istifadə olunur:
\begin(tənlik) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(tənlik) \begin(tənlik) \lim_(\alpha\to(0)) )\frac(\arcsin\alpha)(\alpha)=1 \end(tənlik) \begin(tənlik) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(tənlik)
On bir nümunə bu səhifədə həll olunur. 1 nömrəli misal (2)-(4) düsturlarının isbatına həsr edilmişdir. Nümunələr #2, #3, #4 və #5 ətraflı şərhlərlə həlləri ehtiva edir. 6-10-cu misallarda təfərrüatlı izahatlar əvvəlki nümunələrdə verildiyi üçün az və ya heç bir şərh verilməyən həllər var. Həll edərkən tapıla bilən bəzi triqonometrik düsturlardan istifadə olunur.
Qeyd edim ki, triqonometrik funksiyaların mövcudluğu, $\frac (0) (0)$ qeyri-müəyyənliyi ilə birlikdə, ilk diqqətəlayiq həddi tətbiq etmək lazım olduğunu ifadə etmir. Bəzən sadə triqonometrik çevrilmələr kifayətdir - məsələn, bax.
Nümunə №1
Sübut edin ki, $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$ olduğundan, onda:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
$\lim_(\alpha\to(0))\cos(0)=1$ və $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ olduğundan, sonra:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \ frac (\ sin (\ alfa)) (\ alfa)) (\ displaystyle \ lim_ (\ alfa \ to (0)) \ cos (\ alfa)) =\ frac (1) (1) =1. $$
b) $\alpha=\sin(y)$ əvəzini edək. $\sin(0)=0$ olduğundan, $\alpha\to(0)$ şərtindən bizdə $y\to(0)$ olur. Bundan əlavə, $\arcsin\alpha=\arcsin(\sin(y))=y$ olduğu sıfırın qonşuluğu var, belə ki:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
$\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ bərabərliyi sübut edilmişdir.
c) $\alpha=\tg(y)$ əvəzini edək. $\tg(0)=0$ olduğundan, $\alpha\to(0)$ və $y\to(0)$ şərtləri ekvivalentdir. Bundan əlavə, $\arctg\alpha=\arctg\tg(y))=y$ olduğu sıfır məhəlləsi var, buna görə də a) nöqtəsinin nəticələrinə əsaslanaraq, əldə edəcəyik:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
$\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ bərabərliyi sübut edilmişdir.
a), b), c) bərabərlikləri tez-tez ilk əlamətdar həddi ilə birlikdə istifadə olunur.
Nümunə №2
Hesablama limiti $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.
Çünki $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ və $\lim_( x) \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, yəni və kəsrin payı və məxrəci eyni vaxtda sıfıra meyllidir, onda burada biz $\frac(0)(0)$ formasının qeyri-müəyyənliyi ilə məşğul oluruq, yəni. edildi. Bundan əlavə, sinus işarəsinin altındakı və məxrəcdəki ifadələrin eyni olduğunu görmək olar (yəni, təmin olunur):
Beləliklə, səhifənin əvvəlində qeyd olunan hər iki şərt yerinə yetirilir. Buradan belə çıxır ki, formula tətbiq olunur, yəni. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\sağ))(\frac(x^2-4)(x+ 7) ))=1$.
Cavab verin: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\sağ))(\frac(x^2-4)(x +7))=1$.
Nümunə №3
$\lim_(x\to(0))\frac(\sin(9x))(x)$ tapın.
$\lim_(x\to(0))\sin(9x)=0$ və $\lim_(x\to(0))x=0$ olduğundan, biz $\frac( formasının qeyri-müəyyənliyi ilə məşğul oluruq. 0 )(0)$, yəni, edildi. Lakin sinus işarəsinin altındakı və məxrəcdəki ifadələr uyğun gəlmir. Burada məxrəcdəki ifadəni istədiyiniz formaya uyğunlaşdırmaq tələb olunur. Məxrəcdə olmaq üçün bizə $9x$ ifadəsi lazımdır - o zaman doğru olacaq. Prinsipcə, məxrəcdə $9$ faktorunu əldən vermişik, bunu daxil etmək o qədər də çətin deyil, məxrəcdəki ifadəni $9$-a vurmaq kifayətdir. Təbii ki, vurmanı $9$-a kompensasiya etmək üçün dərhal $9$-a bölməli və bölməli olacaqsınız:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin) (9x))(9x) $$
İndi məxrəcdəki və sinus işarəsinin altındakı ifadələr eynidir. $\lim_(x\to(0))\frac(\sin(9x))(9x)$ limitinin hər iki şərti təmin edilir. Beləliklə, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Və bu o deməkdir ki:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Cavab verin: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Nümunə №4
$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$ tapın.
$\lim_(x\to(0))\sin(5x)=0$ və $\lim_(x\to(0))\tg(8x)=0$ olduğundan, burada biz qeyri-müəyyənliyi ilə məşğul oluruq. $\frac(0)(0)$ forması. Ancaq ilk diqqətəlayiq hədd forması pozulur. Tərkibində $\sin(5x)$ olan pay məxrəcdə $5x$ tələb edir. Bu vəziyyətdə, ən asan yol, payı $5x$-a bölmək və dərhal $5x$-a vurmaqdır. Bundan əlavə, $\tg(8x)$-nı $8x$-a vurub bölmək üçün məxrəclə oxşar əməliyyat həyata keçirəcəyik:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\sağ| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
$x$ azaldıb $\frac(5)(8)$ sabitini limit işarəsindən çıxarsaq, əldə edirik:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Qeyd edək ki, $\lim_(x\to(0))\frac(\sin(5x))(5x)$ birinci əlamətdar həddi tələblərə tam cavab verir. $\lim_(x\to(0))\frac(\tg(8x))(8x)$ tapmaq üçün aşağıdakı düstur tətbiq edilir:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to) (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Cavab verin: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Nümunə №5
$\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$ tapın.
$\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (xatırlayın ki, $\cos(0)=1$) və $\ lim_(x\to(0))x^2=0$, onda biz $\frac(0)(0)$ formasının qeyri-müəyyənliyi ilə məşğul oluruq. Bununla belə, ilk gözəl həddi tətbiq etmək üçün sinuslara (sonra düsturu tətbiq etmək üçün) və ya tangenslərə (sonra düsturu tətbiq etmək üçün) keçərək saydakı kosinusdan xilas olmalısınız. Bunu aşağıdakı transformasiya ilə edə bilərsiniz:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\sağ)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\sol(1-\cos^2(5x)\sağ)=\cos(5x)\cdot\sin^2(5x).$$
Gəlin limitə qayıdaq:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\sol(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\sağ) $$
$\frac(\sin^2(5x))(x^2)$ fraksiyası artıq ilk əlamətdar hədd üçün tələb olunan formaya yaxındır. Gəlin $\frac(\sin^2(5x))(x^2)$ kəsri ilə bir az işləyək, onu ilk əlamətdar həddə uyğunlaşdıraq (qeyd edək ki, saydakı və sinusun altındakı ifadələr uyğun olmalıdır):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\sol(\frac(\sin(5x))(5x)\sağ)^2$$
Nəzərə alınan limitə qayıdaq:
$$ \lim_(x\to(0))\sol(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\sağ) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\sağ)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\sağ)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Cavab verin: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Nümunə №6
$\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$ limitini tapın.
$\lim_(x\to(0))(1-\cos(6x))=0$ və $\lim_(x\to(0))(1-\cos(2x))=0$ olduğundan, onda biz $\frac(0)(0)$ qeyri-müəyyənliyi ilə məşğul oluruq. İlk diqqətəlayiq limitin köməyi ilə onu açaq. Bunun üçün kosinuslardan sinuslara keçək. $1-\cos(2\alpha)=2\sin^2(\alpha)$ olduğundan, onda:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Verilmiş həddi sinuslara keçsək, əldə edəcəyik:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\sol(\) frac(\sin(3x))(3x)\sağ)^2\cdot(9x^2))(\sol(\frac(\sin(x))(x)\sağ)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\sol(\frac(\sin(3x))(3x)\sağ)^2)(\displaystyle\lim_(x) \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Cavab verin: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Nümunə №7
$\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ limitini hesablayın $\alpha\neq\ beta $.
Daha əvvəl ətraflı izahatlar verilmişdi, lakin burada sadəcə qeyd edirik ki, yenə $\frac(0)(0)$ qeyri-müəyyənliyi var. Düsturdan istifadə edərək kosinuslardan sinuslara keçək
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Yuxarıdakı düsturdan istifadə edərək, əldə edirik:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\sağ| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\sağ)\cdot\sin\sol(x\cdot\frac(\alpha-\beta)(2)\sağ))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\sağ))(x)\cdot\frac(\sin\left(x\cdot\frac) (\alfa-\beta)(2)\sağ))(x)\sağ)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\sağ))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\sağ))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\sağ)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\sağ))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\sağ))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alfa^2)(2). $$
Cavab verin: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.
Nümunə №8
$\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$ limitini tapın.
$\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (xatırlayın ki, $\sin(0)=\tg(0)=0$) və $\ lim_(x\to(0))x^3=0$, onda biz burada $\frac(0)(0)$ formasının qeyri-müəyyənliyi ilə məşğul oluruq. Gəlin bunu belə bölək:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\sağ))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\sağ))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\sağ)^2\cdot\frac(1)(\cos(x))\sağ) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Cavab verin: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Nümunə №9
$\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$ limitini tapın.
Çünki $\lim_(x\to(3))(1-\cos(x-3))=0$ və $\lim_(x\to(3))(x-3)\tg\frac(x -) 3)(2)=0$, onda $\frac(0)(0)$ formasının qeyri-müəyyənliyi var. Onun genişləndirilməsinə keçməzdən əvvəl dəyişəni elə dəyişmək rahatdır ki, yeni dəyişən sıfıra meyl etsin (düsturlarda $\alpha \to 0$ dəyişənini qeyd edin). Ən asan yol $t=x-3$ dəyişənini təqdim etməkdir. Bununla belə, sonrakı çevrilmələrin rahatlığı üçün (bu faydanı aşağıdakı həll prosesində görmək olar) aşağıdakı əvəzetməni etməyə dəyər: $t=\frac(x-3)(2)$. Qeyd edim ki, bu halda hər iki əvəzetmə tətbiq oluna bilər, sadəcə ikinci əvəzetmə fraksiyalarla daha az işləməyə imkan verəcək. $x\to(3)$ olduğundan, sonra $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\sağ| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin) (t)\cos(t))(t) =\lim_(t\to(0))\sol(\frac(\sin(t))(t)\cdot\cos(t)\sağ) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Cavab verin: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Nümunə №10
Limiti tapın $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2 )$.
Yenə biz $\frac(0)(0)$ qeyri-müəyyənliyi ilə məşğul oluruq. Onun genişləndirilməsinə keçməzdən əvvəl dəyişəni elə dəyişmək rahatdır ki, yeni dəyişən sıfıra meyl etsin (qeyd edək ki, dəyişən düsturlarda $\alpha\to(0)$-dır). Ən asan yol $t=\frac(\pi)(2)-x$ dəyişənini təqdim etməkdir. $x\to\frac(\pi)(2)$ olduğundan, sonra $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\sol(\frac(\pi)(2)-x\sağ)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\sağ))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\sağ)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Cavab verin: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\sağ)^2) =\frac(1)(2)$.
Nümunə №11
Limitləri tapın $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\) pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
Bu halda ilk gözəl limitdən istifadə etmək məcburiyyətində deyilik. Diqqət edin: həm birinci, həm də ikinci həddlərdə yalnız var triqonometrik funksiyalar və nömrələr. Çox vaxt bu cür nümunələrdə limit işarəsi altında yerləşən ifadəni sadələşdirmək mümkündür. Bu zaman qeyd olunan sadələşdirmə və bəzi amillərin azaldılmasından sonra qeyri-müəyyənlik aradan qalxır. Mən bu nümunəni yalnız bir məqsədlə verdim: triqonometrik funksiyaların limit işarəsi altında olmasının mütləq birinci əlamətdar limitin tətbiqi demək olmadığını göstərmək.
$\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ olduğundan (xatırlayın ki, $\sin\frac(\pi)(2)=1$) və $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (xatırlayın ki, $\cos\frac(\pi)(2)=0$), onda qeyri-müəyyənliklə məşğul oluruq $\frac(0)(0)$ şəklində. Ancaq bu, heç də o demək deyil ki, ilk diqqətəlayiq həddi istifadə etməliyik. Qeyri-müəyyənliyi aşkar etmək üçün onu nəzərə almaq kifayətdir ki, $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Demidoviçin həll kitabında (No 475) oxşar həll var. İkinci limitə gəlincə, bu bölmənin əvvəlki nümunələrində olduğu kimi, bizdə $\frac(0)(0)$ formasının qeyri-müəyyənliyi var. Niyə yaranır? $\tg\frac(2\pi)(3)=-\sqrt(3)$ və $2\cos\frac(2\pi)(3)=-1$ olduğuna görə yaranır. Bu dəyərləri say və məxrəcdəki ifadələri çevirmək üçün istifadə edirik. Hərəkətlərimizin məqsədi: ədədi və məxrəcdəki cəmini hasil olaraq yazın. Yeri gəlmişkən, tez-tez dəyişəni oxşar formada əvəz etmək rahatdır ki, yeni dəyişən sıfıra meyl etsin (məsələn, bu səhifədə 9 və ya 10 nömrəli nümunələrə baxın). Bununla belə, bu misalda dəyişəni əvəz etməyin mənası yoxdur, baxmayaraq ki, istəsəniz $t=x-\frac(2\pi)(3)$ dəyişəninin dəyişdirilməsini həyata keçirmək asandır.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\sol(\cos(x)+\frac(1)(2)\sağ )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\sol(\ cos(x)-\cos\frac(2\pi)(3)\sağ))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin) \sol(x-\frac(2\pi)(3)\sağ))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac) (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3) ))\frac(\sin\left(x-\frac(2\pi)(3)\sağ))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac) (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3) ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3) ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\sağ)\cdot\left( -\frac(1)(2)\sağ)) =-\frac(4 )(\sqrt(3)). $$
Gördüyünüz kimi, ilk gözəl limiti tətbiq etməli deyildik. Əlbəttə ki, istəsən, bu edilə bilər (aşağıdakı qeydə baxın), lakin bu lazım deyil.
İlk əlamətdar limitdən istifadə edərək həll yolu nə olardı? göstərmək/gizlətmək
İlk əlamətdar həddi istifadə edərək, əldə edirik:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\sol(x-\frac(2\pi)(3)\sağ))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi) )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ sağda))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\ frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\sağ) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\sağ)\cdot\left(-\frac(1)(2)\sağ)) =-\frac(4)(\sqrt( 3)). $$
Cavab verin: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Bir neçə gözəl məhdudiyyət var, lakin ən məşhurları birinci və ikinci gözəl həddlərdir. Bu məhdudiyyətlərin diqqətəlayiq cəhəti ondan ibarətdir ki, onlar geniş şəkildə istifadə olunur və çoxsaylı problemlərdə rast gəlinən digər məhdudiyyətləri tapmaq üçün istifadə oluna bilər. Bu dərsin praktiki hissəsində bunu edəcəyik. Problemləri birinci və ya ikinci əlamətdar həddə endirməklə həll etmək üçün onlarda olan qeyri-müəyyənlikləri açıqlamaq lazım deyil, çünki bu hədlərin dəyərləri çoxdan böyük riyaziyyatçılar tərəfindən çıxarılmışdır.
İlk diqqətəlayiq hədd sonsuz kiçik bir qövsün sinüsünün eyni qövsə nisbətinin həddi radian ölçüsü ilə ifadə edilir:
Gəlin ilk diqqətəlayiq həddə problemlərin həllinə keçək. Qeyd: triqonometrik funksiya limit işarəsinin altındadırsa, bu, demək olar ki, bu ifadənin ilk əlamətdar həddə endirilə biləcəyinə əmin bir işarədir.
Misal 1 Həddini tapın.
Həll. Əvəzində əvəzetmə x sıfır qeyri-müəyyənliyə səbəb olur:
![]() .
.
Məxrəc sinusdur, buna görə də ifadə ilk diqqətəlayiq həddə endirilə bilər. Transformasiyaya başlayaq:
![]() .
.
Məxrəcdə - üç x-in sinüsü və paylayıcıda yalnız bir x var, bu o deməkdir ki, payda üç x almaq lazımdır. Nə üçün? Təqdim etmək 3 x = a və ifadəni əldə edin.
Və biz ilk diqqətəlayiq həddin dəyişikliyinə gəlirik:
çünki bu düsturda x yerinə hansı hərfin (dəyişən) olmasının əhəmiyyəti yoxdur.
x-i üçə vurub dərhal bölürük:
 .
.
Qeyd olunan ilk əlamətdar həddə uyğun olaraq, kəsr ifadəsini əvəz edirik:
İndi nəhayət bu limiti həll edə bilərik:
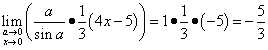 .
.
Misal 2 Həddini tapın.
Həll. Birbaşa əvəzetmə yenə də "sıfırın sıfıra bölünməsi" qeyri-müəyyənliyinə gətirib çıxarır:
![]() .
.
İlk diqqətəlayiq həddi əldə etmək üçün saydakı sinus işarəsinin altındakı x-in və məxrəcdəki sadəcə x-in eyni əmsalla olması lazımdır. Bu əmsal 2-yə bərabər olsun. Bunun üçün x-dəki cari əmsalı aşağıdakı kimi təsəvvür edək, kəsrlərlə hərəkətlər edərək, əldə edirik:
 .
.
Misal 3 Həddini tapın.
Həll. Əvəz edərkən, yenidən qeyri-müəyyənliyi "sıfıra bölünən sıfır" alırıq:
 .
.
Yəqin ki, siz artıq başa düşürsünüz ki, ilkin ifadədən ilk gözəl həddi birinci gözəl həddə vuraraq əldə edə bilərsiniz. Bunun üçün paydakı x-in və məxrəcdəki sinüsün kvadratlarını eyni amillərə parçalayırıq və x və sinus üçün eyni əmsalları əldə etmək üçün paydakı x-i 3-ə bölürük və dərhal 3-ə vurun. Alırıq:
 .
.
Misal 4 Həddini tapın.
Həll. Yenə "sıfırın sıfıra bölünməsi" qeyri-müəyyənliyini alırıq:
![]() .
.
İlk iki əlamətdar həddin nisbətini əldə edə bilərik. Həm payı, həm də məxrəci x-ə bölürük. Sonra sinuslarda və x-də əmsalların üst-üstə düşməsi üçün yuxarı x-i 2-yə vurub dərhal 2-yə, aşağı x-i 3-ə vurub dərhal 3-ə bölürük.

Misal 5 Həddini tapın.
Həll. Və yenə də “sıfırın sıfıra bölünməsi” qeyri-müəyyənliyi:
Triqonometriyadan xatırlayırıq ki, tangens sinusun kosinusa nisbətidir və sıfırın kosinusu birə bərabərdir. Transformasiyalar edirik və əldə edirik:
 .
.
Misal 6 Həddini tapın.
Həll. Limit işarəsi altındakı triqonometrik funksiya yenidən ilk əlamətdar həddi tətbiq etmək fikrini təklif edir. Biz onu sinusun kosinusa nisbəti kimi təqdim edirik.
İlk diqqətəlayiq hədd belə görünür: lim x → 0 sin x x = 1 .
Praktik nümunələrdə ilk diqqətəlayiq həddin modifikasiyalarına tez-tez rast gəlinir: lim x → 0 sin k · x k · x = 1 , burada k bəzi əmsaldır.
İzah edək: lim x → 0 sin (k x) k x = boş t = k x və x-dən → 0-dan sonra t → 0 = lim t → 0 sin (t) t = 1 .
İlk diqqətəlayiq məhdudiyyətin nəticələri:
- lim x → 0 x sin x = lim x → 0 = 1 sin x x = 1 1 = 1
- lim x → 0 k x sin k x = lim x → 0 1 sin (k x) k x = 1 1 = 1
Bu nəticələri L'Hospital qaydasını və ya sonsuz kiçik funksiyaların dəyişməsini tətbiq etməklə sübut etmək kifayət qədər asandır.
Birinci əlamətdar həddi nəzərə alaraq həddi tapmağın bəzi problemlərini nəzərdən keçirək; verək Ətraflı Təsviri həllər.
Misal 1
L'Hopital qaydasından istifadə etmədən həddi müəyyən etmək lazımdır: lim x → 0 sin (3 x) 2 x .
Həll
Dəyəri əvəz edin:
lim x → 0 sin (3 x) 2 x = 0 0
Biz görürük ki, sıfırın sıfıra bölünməsi ilə bağlı qeyri-müəyyənlik var. Həll metodunu müəyyən etmək üçün qeyri-müəyyənliklər cədvəlinə baxın. Sinus və onun arqumentinin birləşməsi bizə ilk gözəl limitin istifadəsi haqqında ipucu verir, lakin əvvəlcə ifadəni çevirək. Kəsrin payını və məxrəcini 3 x-ə vururuq və alırıq:
lim x → 0 sin (3 x) 2 x = 0 0 = lim x → 0 3 x sin (3 x) 3 x (2 x) = lim x → 0 sin (3 x) 3 x 3 x 2 x = = lim x → 0 3 2 sin (3 x) 3 x
Birinci diqqətəlayiq həddin nəticəsi əsasında bizdə var: lim x → 0 sin (3 x) 3 x = 1 .
Sonra nəticəyə gəlirik:
lim x → 0 3 2 sin (3 x) 3 x = 3 2 1 = 3 2
Cavab: lim x → 0 sin (3 x) 3 x = 3 2 .
Misal 2
lim x → 0 1 - cos (2 x) 3 x 2 həddi tapmaq lazımdır.
Həll
Dəyərləri əvəz edin və əldə edin:
lim x → 0 1 - cos (2 x) 3 x 2 = 1 - cos (2 0) 3 0 2 = 1 - 1 0 = 0 0
Sıfırın qeyri-müəyyənliyini sıfıra böldükdə görürük. Gəlin triqonometriya düsturlarından istifadə edərək payı çevirək:
lim x → 0 1 - cos (2 x) 3 x 2 = 0 0 = lim x → 0 2 sin 2 (x) 3 x 2
Görürük ki, indi burada ilk diqqətəlayiq həddi tətbiq etmək mümkündür:
lim x → 0 2 sin 2 (x) 3 x 2 = lim x → 0 2 3 sin x x sin x x = 2 3 1 1 = 2 3
Cavab: lim x → 0 1 - cos (2 x) 3 x 2 = 2 3 .
Misal 3
lim x → 0 a r c sin (4 x) 3 x həddi hesablamaq lazımdır.
Həll
Dəyəri əvəz edin:
lim x → 0 a r c sin (4 x) 3 x = a r c sin (4 0) 3 0 = 0 0
Sıfırın sıfıra bölünməsinin qeyri-müəyyənliyini görürük. Əvəz edək:
arc sin (4 x) = t ⇒ sin (arc sin (4 x)) = sin (t) 4 x = sin (t) ⇒ x = 1 4 sin (t) lim x → 0 (arc sin (4 x) ) \u003d arc sin (4 0) \u003d 0, sonra t → 0 kimi x → 0.
Bu halda, dəyişəni dəyişdirdikdən sonra limit aşağıdakı formanı alır:
lim x → 0 a r c sin (4 x) 3 x = 0 0 = lim t → 0 t 3 1 4 sin (t) = = lim t → 0 4 3 t sin t = 4 3 1 = 4 3
Cavab: lim x → 0 a r c sin (4 x) 3 x = 4 3 .
Məqalənin materialını daha dolğun başa düşmək üçün “Limitlər, əsas təriflər, tapma nümunələri, vəzifələr və həllər” mövzusunun materialını təkrarlamaq lazımdır.
Mətndə səhv görsəniz, onu vurğulayın və Ctrl+Enter düymələrini basın





